题目内容
9.已知直线l1:4x-3y+6=0和直线${l_2}:x=-\frac{p}{2}$,若抛物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.(1)求抛物线C的方程;
(2)在抛物线C上恒有两点关于直线y=kx+3对称,求k的取值范围.
分析 (1)由抛物线的定义知:P到直线${l_2}:x=-\frac{p}{2}$的距离等等于P到焦点的距离,则P距离之和的最小值为点F到直线l1的距离,利用点到直线的距离公式,即可求得p的值,求得抛物线C的方程;
(2)可设直线AB:x=-ky+m.代入抛物线方程,由韦达定理及中点坐标公式可知:$m=-\frac{{2{k^3}+2k+3}}{k}$.又AB与抛物线有两个不同的交点,故△=16k2+16m>0.代入即可求得k的取值范围.
解答 解:(1)抛物线C:y2=2px(p>0)焦点在x轴上,焦点F($\frac{p}{2}$,0),
由抛物线的定义知:P到直线${l_2}:x=-\frac{p}{2}$的距离等等于P到焦点的距离,
∴P到两直线的距离之和的最小值为点F到直线l1的距离,
由点到直线的距离公式可知:$\frac{丨2p+6丨}{\sqrt{{4}^{2}+{3}^{2}}}$=2,解得:p=2,
∴抛物线的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),关于直线y=kx+3对称,
故可设直线AB:x=-ky+m.
$\left\{\begin{array}{l}{x=-ky+m}\\{{y}^{2}=4x}\end{array}\right.$,整理得:y2+4ky-4m=0.
由韦达定理可知:y1+y2=-4m,则${y_0}=\frac{{{y_1}+{y_2}}}{2}=-2k$,
∴${x_0}=-k{y_0}+m=2{k^2}+m$.
∵点M(x0,y0)在y=kx+3上,则-2k=k(2k2+m)+3.即$m=-\frac{{2{k^3}+2k+3}}{k}$.
又AB与抛物线有两个不同的交点,故△=16k2+16m>0.
将m代入上式得:$\frac{{k}^{3}+2k+3}{k}$,即k(k+1)(k2-k+3)<0,
k2-k+3>0恒成立,
∴解得:-1<k<0,
由故k的取值范围为(-1,0).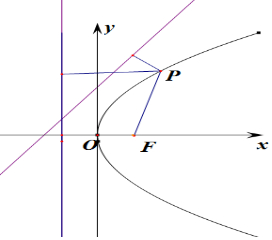
点评 本题考查抛物线的标准方程,直线与抛物线的位置关系,考查韦达定理,中点坐标公式及判别式的应用,考查计算能力,属于中档题.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案| 少数民族 | 少数民族学生人数(单位:人) | 抽取人数(单位:人) |
| 回族 | 18 | x |
| 彝族 | 36 | 2 |
| 白族 | 54 | y |
(Ⅱ)若从彝族、白族抽取的学生中选2人作专题发言,求这二人都来自白族的概率.
| A. | 2 | B. | $\frac{5}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |