题目内容
某厂生产某种产品的固定成本(固定投入)为2500元,已知每生产x件这样的产品需要再增加可变成本C(x)=200x+
x3(元),若生产出的产品都能以每件500元售出,要使利润最大,该厂应生产多少件这种产品?最大利润是多少?
| 1 | 36 |
分析:先由题意建立利润L(x)的函数关系式,然后利用导数求函数的最值.
解答:解:设该厂生产x件这种产品的利润为L(x)元,则L(x)=500x-2500-C(x)=500x-2500-(200x+
x3)
=300x-
x3-2500,x∈N,则L′(x)=300-
x2,则由L′(x)=300-
x2=0,解得x=60(件).
又当0≤x<60时,L'(x)>0,函数L(x)单调递增,
当x>60时,L'(x)<0,函数L(x)单调递减,
所以x=60是函数L(x)的极大值点,同时也是最大值点,所以当x=60时,L(x)=9500元.
因此,要使利润最大,该厂应生产60件这种产品,最大利润为9500元.
| 1 |
| 36 |
=300x-
| 1 |
| 36 |
| 1 |
| 12 |
| 1 |
| 12 |
又当0≤x<60时,L'(x)>0,函数L(x)单调递增,
当x>60时,L'(x)<0,函数L(x)单调递减,
所以x=60是函数L(x)的极大值点,同时也是最大值点,所以当x=60时,L(x)=9500元.
因此,要使利润最大,该厂应生产60件这种产品,最大利润为9500元.
点评:本题的考点是利用导数解决生活中的优化问题,先建立函数关系,然后利用导数最值,要注意若函数在定义域内只有一个极值点,那么这个极值点也是最值点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
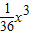 (元),若生产出的产品都能以每件500元售出,要使利润最大,该厂应生产多少件这种产品?最大利润是多少?
(元),若生产出的产品都能以每件500元售出,要使利润最大,该厂应生产多少件这种产品?最大利润是多少?