Question

已知曲线C上任意一点到直线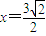的距离与它到点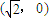的距离之比是．   
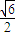（I）求曲线C的方程；
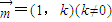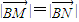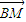（II）设B为曲线C与y轴负半轴的交点，问：是否存在方向向量为的直线l，l与曲线C相交于M、N两点，使，且与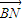夹角为60°？若存在，求出k值，并写出直线l的方程；若不存在，请说明理由．

Answer 1

【答案】分析：（1）由题意可得，欲曲线C的方程，设P（x，y）为曲线C上任意一点，只须求出x，y之间的关系式即可，根据点到点的距离与到直线的距离的比值，可得点的坐标满足的关系式，化简即得；
（2）对于存在性问题，可先假设存在，即假设存在方向向量为的直线l，再设所求直线l：y=kx+m，将直线的方程代入椭圆的方程，消去y得到关于x的一元二次方程，再结合根系数的关系利用弦长公式即可求得m值．若出现矛盾，则说明假设不成立，即不存在；否则存在．
解答：解：（Ⅰ）设P（x，y）为曲线C上任意一点，依题意（2分）
化简：，
∴曲线C为椭圆，其方程为（4分）
（Ⅱ）设直线l：y=kx+m，
由 消去y得：（1+3k²）x²+6kmx+3m²-3=0（6分）
设M（x₁，y₁），N（x₂，y₂），MN中点G（x，y），
则，

=…（ 1）
依题意：，与夹角为60°，
∴△BMN为等边三角形，
∴k_BG•k=-1，即，…（2）
由（2）代入（1）：，
又∵△BMN为等边三角形，∴B到MN距离，
即解得：，m=1，
经检验，m=1使方程有解，所以直线l的方程为：（12分）
点评：本题主要考查了抛物线的定义的灵活应用，解决直线与圆锥曲线的相交的有关问题，一般的思路是将直线与圆锥曲线方程联立，得到关于应该未知数的方程，利用韦达定理来解决．