题目内容

求函数f（x）=在R上的极值（a＞0）.

解：∵f′（x）=，

令f′（x）=0，得x=0，

此外该函数定义域为R，而在x=±a处不可导，因此列表时应将x=±a点考虑进去.

x变化时，y′、y的变化情况如下表：

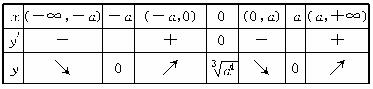
由上表知f（x）在x=±a处取得极小值0，在x=0处取得极大值.

点评：函数在某点x0不可导，但x0点有可能是该函数的极值点.由此可见“有极值但不一定可导”.如y=|x|在x=0处不可导，但x=0是y=|x|的极小值点，再如f（x）=x，x=0不可导，且x=0也不是极值点.总之“x0满足f′（x0）=0”是“x= x0为f（x）的极值点”的既不充分也不必要条件.连续函数的极大值与极小值应间隔出现.

练习册系列答案
相关题目
已知a＞0，设命题p：函数f（x）=ax在R上是增函数，q：不等式x+|x-2a|＞1的解集为R，
（1）若函数y=f（x+1）恒过定点M（1，4），求a
（2）若p和q中有且只有一个命题为真命题，求a的取值范围．
设函数f（x）定义在R上，对于任意实数m、n，恒有f(m+n)=f(m)?f(n)，且当x＞0时，0＜f（x）＜1．
（1）求证：f（0）=1，且当x＜0时，f（x）＞1；
（2）设集合A={(x，y)|f(x2)?f(y2)＞f(1)}，B={（x，y）|f（ax-y+2）=1，a∈R}，若A∩B=∅，求a的取值范围．
（1）求函数f（x）=ex在x=0处的切线方程．
（2）x∈R，证明不等式ex≥x+1．
（2013•虹口区二模）定义域为D的函数f（x），如果对于区间I内（I⊆D）的任意两个数x1、x2都有f(
x1+x2
2
)≥
1
2
[f(x1)+f(x2)]成立，则称此函数在区间I上是“凸函数”．
（1）判断函数f（x）=-x2在R上是否是“凸函数”，并证明你的结论；
（2）如果函数f(x)=x2+
a
x
在区间[1，2]上是“凸函数”，求实数a的取值范围；
（3）对于区间[c，d]上的“凸函数”f（x），在[c，d]上的任取x1，x2，x3，…，x2n，证明：f(
x1+x2+…+x2n
2n
)≥
1
2n
[f(x1)+f(x2)+…+f(x2n)]．
已知函数f（x）=（x2+ax-2a2+3a）ex（x∈R），其中a∈R．
（1）当a=0时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）讨论函数f（x）的单调性；
（3）当a=1时，求函数f（x））在[-3，0]上的最大值和最小值．（参考数据：e≈2.71828，e2≈7.38905）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网