Question

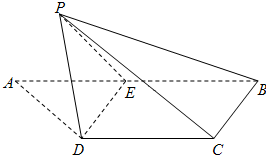
如图，梯形ABCD中，CD∥AB，AD=DC=CB=AB，E是AB的中点，将△ADE沿DE折起，使点A折到点P的位置，且二面角P-DE-C的大小为120°．

(Ⅰ)求证：DE∥平面PBC；

(Ⅱ)求证：DE⊥PC；

(Ⅲ)求直线PD与平面BCDE所成角的正弦值．

Answer 1

证明：(Ⅰ)∵E是AB的中点，∴BE=AB，

又∵CD∥AB，DC=AB，∴DC∥EB且DC=EB，

∴四边形DCBE是平行四边形，∴ED∥BC．

∵DE面PBC，BE面PBC，∴DE∥平面PBC．

(Ⅱ)连接EC，据(Ⅰ)知，CD∥AE且CD=AE，

∴四边形ADCE为平行四边形，

又AD=DC,∴四边形ADCE是菱形．

连接AC交DE于F，连接PF，

则DE⊥AC，DE⊥PF，

∵AC∩PF=F，∴DE⊥平面PFC，

又∵PC平面PFC，∴DE⊥PC．

(Ⅲ)∵DE⊥平面PFC，DE平面BCDE,

∴平面PFC⊥平面BCDE，且两平面交于AC．

过点P作PH⊥AC于H，则PH⊥平面BCDE，连接DH，则DH为PD在平面BCDE上的射影，∴∠PDH就是直线PD与平面BCDE所成的角．

由(Ⅱ)知，∠PFC就是二面角P-DE-C的平面角，

∴∠PFC=120°，∴∠PFA=60°．

设AD=AE=BC=DE=a，则AF=PF=a，

在Rt△PHF中，PH=PF·sin60°=a.

∴在Rt△PHD中， sin∠PDH=．