题目内容
求解不等式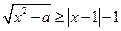
。
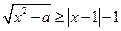。当
时，有
；当
时，有
；当
时，
。
时，有；当时，有；当时，。（I）
情形。此时不等式为
。
于是有
（1）
。
因此 当时，有
；当
时，有；
当
时，有
；当时，空集。
（2）
。
此时有 当时，有
；当时，有；当时，有；当时，。
（II）
情形。此时不等式为
。
于是有
（3）
。
因此 当时，有
；当时，有
；当
时，空集。
（4）
。
因此 当时，有
；当
时，空集。
综合（1）－（4）可得
当时，有；当时，有；当时，。
情形。此时不等式为。于是有
（1）
。因此 当
时，有；当时，有；当
时，有；当时，空集。 （2）
。此时有 当
时，有；当时，有；当时，有；当时，。 （II）
情形。此时不等式为。于是有
（3）
。因此 当
时，有；当时，有；当时，空集。（4）
。 因此 当
时，有；当时，空集。综合（1）－（4）可得
当
时，有；当时，有；当时，。
练习册系列答案
相关题目
的解集是（ ）
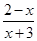＞0的解集为___________．
的解集为 .
≤x－1的解集是( )
的解集为 。
的定义域为A， 
的定义域为B.（1）求A； （2）若
，求实数a的取值范围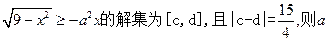
= 。