题目内容
数列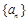 中各项为正数,
中各项为正数,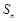 为其前n项和,对任意
为其前n项和,对任意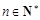 ,总有
,总有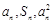 成等差数列.
成等差数列.
(1)求数列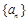 的通项公式;
的通项公式;
(2)是否存在最大正整数p,使得命题“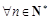 ,
,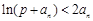 ”是真命题?若存在,求出p;若不存在,请说明理由.
”是真命题?若存在,求出p;若不存在,请说明理由.
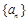 中各项为正数,
中各项为正数,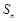 为其前n项和,对任意
为其前n项和,对任意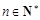 ,总有
,总有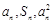 成等差数列.
成等差数列.(1)求数列
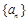 的通项公式;
的通项公式;(2)是否存在最大正整数p,使得命题“
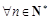 ,
,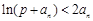 ”是真命题?若存在,求出p;若不存在,请说明理由.
”是真命题?若存在,求出p;若不存在,请说明理由.(1)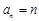 ;(2)详见解析.
;(2)详见解析.
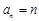 ;(2)详见解析.
;(2)详见解析.试题分析:(1)根据
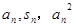 是等差数列,得到
是等差数列,得到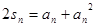 ,当
,当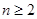 时,
时,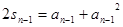 两式相减整理得到关于数列
两式相减整理得到关于数列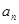 的递推公式,可以知道数列
的递推公式,可以知道数列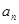 是等差数列,利用
是等差数列,利用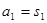 求出首项;
求出首项;(2)第一种方法就是首先假设存在正整数
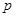 ,满足
,满足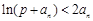 ,利用
,利用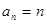 代入得
代入得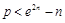 成立即
成立即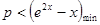 中的最大整数,设
中的最大整数,设 ,
,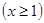 ,利用导数易知函数的单调性,易求函数的最小值,
,利用导数易知函数的单调性,易求函数的最小值,第二种方法设函数
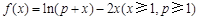 ,求其导数,得到函数是单调递增函数,其最大值小于0,求出p的范围.
,求其导数,得到函数是单调递增函数,其最大值小于0,求出p的范围.试题解析:(1)由已知
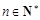 时,
时,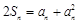 ,∴
,∴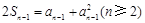
两式相减,得
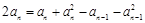 ∴
∴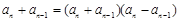
又
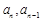 为正数,∴
为正数,∴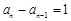
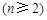 . 4分
. 4分∴
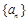 是公差为1的等差数列.
是公差为1的等差数列.当
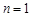 时,
时,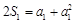 ,得
,得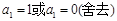 ,∴
,∴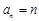 . 6分
. 6分(2)解法1:假设存在正整数p,满足
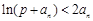 ,即
,即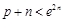 .
.∴
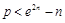
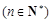 8分
8分设函数
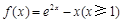 ,则
,则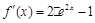 .
.当
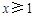 时,
时,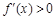 ,∴
,∴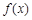 在[1,+∞)上为增函数.
在[1,+∞)上为增函数.∴
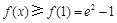 ,即有
,即有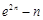
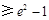 .
.∵p为满足
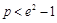 的最大正整数,而
的最大正整数,而 ,故
,故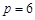 . 12分
. 12分解法2:设
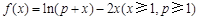 ,
, ,
,故
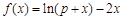 在[1,+∞)上为减函数, 9分
在[1,+∞)上为减函数, 9分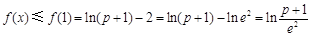 .
.令
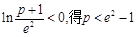 . ∵
. ∵ ,
,故使
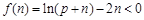 成立的最大正整数
成立的最大正整数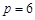 . 12分
. 12分 求
求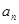 ;2.利用函数的导数求其最值.
;2.利用函数的导数求其最值.
练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
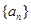 的首项
的首项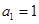 ,公差
,公差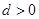 ,且第
,且第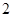 项、第
项、第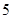 项、第
项、第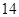 项分别是等比数列
项分别是等比数列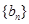 的第
的第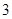 项、第
项、第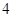 项.
项.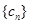 对
对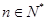 ,均有
,均有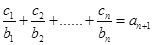 成立,求
成立,求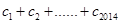 .
.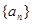 的前n项和为Sn,且满足
的前n项和为Sn,且满足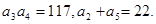
 的前
的前 项和为
项和为 ,且满足
,且满足 ,则
,则 ;
; 的前
的前 ,若在每相邻两项之间各插入一个数,使之成为等差数列,那么新的等差数列的公差是________.
,若在每相邻两项之间各插入一个数,使之成为等差数列,那么新的等差数列的公差是________.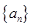 满足条件
满足条件 , 则
, 则 .
.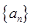 ,对任意的
,对任意的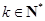 ,当
,当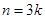 时,
时,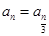 ;当
;当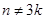 时,
时,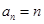 ,那么该数列中的第10个2是该数列的第 项.
,那么该数列中的第10个2是该数列的第 项. 满足:
满足: ,则其前10项的和
,则其前10项的和 ( )
( )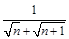 ,若前n项和为10,则项数n为( )
,若前n项和为10,则项数n为( )