题目内容
【题目】已知函数 
的部分图象如图所示.
（1）求函数 
的解析式；
（2）求函数 
的单调递增区间.
【答案】
（1）解：由图象可知，周期 
，∴ 
，
∵点 
在函数图象上，∴ 
，∴ 
，解得， 
， 
， 
，
∵ 
，∴ 
；∵点 
在函数图象上，∴ 
， 
，
∴函数 
的解析式为 
（2）解： 
，
，
由 
， ，得 
，
∴函数 
的单调递增区间为 
，
【解析】(1)根据题意结合已知条件由图像求出A以及周期的值利用周期公式求出 ω再由图像代入点的坐标根据角的特殊值求出 φ进而求出函数 f ( x ) 的解析式。(2)由已知结合两角和差的正弦公式整理原代数式利用正弦函数的单调性由整体思想即可求出单调区间。
【考点精析】关于本题考查的两角和与差的正弦公式和正弦函数的单调性，需要了解两角和与差的正弦公式：
；正弦函数的单调性：在
上是增函数；在
上是减函数才能得出正确答案．
【题目】为了稳定市场，确保农民增收，某农产品7个月份的每月市场收购价格与其前三个月的市场收购价格有关，并使其与前三个月的市场收购价格之差的平方和最小，下表列出的是该产品今年前6个月的市场收购价格，则前7个月该产品的市场收购价格的方差为( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
价格(元/担) | 68 | 78 | 67 | 71 | 72 | 70 |
A.
B.
C.11
D.
【题目】2015年12月，京津冀等地数城市指数“爆表”，北方此轮污染为2015年以来最严重的污染过程．为了探究车流量与PM2.5的浓度是否相关，现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表：
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量x（万辆） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
PM2.5的浓度y（微克/立方米） | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
（Ⅰ）由散点图知y与x具有线性相关关系，求y关于x的线性回归方程；
（Ⅱ）（ⅰ）利用（Ⅰ）所求的回归方程，预测该市车流量为8万辆时PM2.5的浓度；
（ⅱ）规定：当一天内PM2.5的浓度平均值在（0，50]内，空气质量等级为优；当一天内PM2.5的浓度平均值在（50，100]内，空气质量等级为良．为使该市某日空气质量为优或者为良，则应控制当天车流量在多少万辆以内？（结果以万辆为单位，保留整数．）
参考公式：回归直线的方程是 
= 
x+ 
，其中 = 
， = 
﹣ 
．
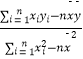