题目内容
若x＞1，不等式x+| 1 | x-1 |
分析：由于 x+
=x-1+
+1≥3，不等式x+
≥k恒成立，故k≤3，从而得到实数k的最大值．
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x-1 |
解答：解：∵x＞1，x+
=x-1+
+1≥2+1=3，不等式x+
≥k恒成立，
∴k≤3，∴实数k的最大值是 3，
故答案为：3．
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x-1 |
∴k≤3，∴实数k的最大值是 3，
故答案为：3．
点评：本题考查基本不等式的应用，注意检验等号成立的条件，式子的变形是解题的关键．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
；
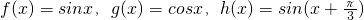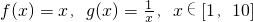的线性生成函数h（x），其中a＞0，b＞0．若h（x）≥b对a∈[1，2]恒成立，求实数b的取值范围．
；
的线性生成函数h（x），其中a＞0，b＞0．若h（x）≥b对a∈[1，2]恒成立，求实数b的取值范围．
.
(k≥0)恒成立,求实数k的取值范围;
,x∈(0,+∞),数列{an}满足a1=1,an+1=f(an);数列{bn}满足b1=1,bn+1=
,其中Sn为数列{bn}的前n项和,n=1,2,3,….
,证明Tn＜3.
≥k恒成立，则实数k的最大值是 ．