题目内容
已知椭圆C：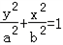
（a＞b＞0）的离心率为
，过右顶点A 的直线l与椭圆C相交于A、B两点，且B（﹣1，﹣3）．
（1）求椭圆C和直线l的方程；
（2）若圆D：x2﹣2mx+y2+4y+m2﹣4=0与直线lAB相切，求实数m的值．
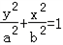（a＞b＞0）的离心率为，过右顶点A 的直线l与椭圆C相交于A、B两点，且B（﹣1，﹣3）．（1）求椭圆C和直线l的方程；
（2）若圆D：x2﹣2mx+y2+4y+m2﹣4=0与直线lAB相切，求实数m的值．
解：（1）由题意，
，
∴
，
∴椭圆C的方程为
；
∵右顶点A（2，0），B（﹣1，﹣3）
∴直线l的方程为x﹣y﹣2=0；
（2）圆D：x2﹣2mx+y2+4y+m2﹣4=0的标准方程为：（x﹣m）2+（y+2）2=8
∵圆D：x2﹣2mx+y2+4y+m2﹣4=0与直线lAB相切
∴
∴m=±4
，∴
，∴椭圆C的方程为
；∵右顶点A（2，0），B（﹣1，﹣3）
∴直线l的方程为x﹣y﹣2=0；
（2）圆D：x2﹣2mx+y2+4y+m2﹣4=0的标准方程为：（x﹣m）2+（y+2）2=8
∵圆D：x2﹣2mx+y2+4y+m2﹣4=0与直线lAB相切
∴
∴m=±4
练习册系列答案
相关题目
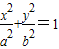（a＞b＞0）的左、右焦点分别为F1（-1，0）、F2（1，0），离心率为
．
（O为坐标原点），求△AOB的面积；
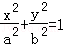（a＞b＞0）的两个焦点分别为F1（﹣1，0），F2（1，0），且椭圆C经过点
．
，求点Q的轨迹方程．
（a＞b＞0）的一个顶点为A（2,0），离心率为
，直线y=k（x-1）与椭圆C交于不同的两点M、N.
时，求k的值.
+
=1(a＞b＞0)，直线y=x+
与以原点为圆心，以椭圆C的短半轴长为半径的圆相切，F1，F2为其左、右焦点，P为椭圆C上任一点，△F1PF2的重心为G，内心为I，且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L：y=kx+m(k≠0)与椭圆C交于不同两点A，B且线段AB的垂直平分线过定点C(
，0)求实数k的取值范围。
（a>b>0）的离心率为
，过右焦点F且斜率为k（k>0）的直线与椭圆C相交于A、B两点，若
。则
（ ） 
（D）