题目内容
已知非零向量 ,
, 满足|
满足| -
- |=|
|=| +
+ |=λ|
|=λ| |(λ≥2),则向量
|(λ≥2),则向量 -
- 与
与 +
+ 的夹角的最大值为________.
的夹角的最大值为________.

分析:设
 =
= ,
, =
= ,OACB为平行四边形,由条件可得平行四边形OACB为矩形,设|
,OACB为平行四边形,由条件可得平行四边形OACB为矩形,设| |=1,则 OA=
|=1,则 OA=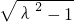 .由余弦定理求得cos∠CDA=
.由余弦定理求得cos∠CDA=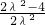 =1-
=1- ≥
≥ ,由此可得∠CDA 的最大值,此最大值即为所求.
,由此可得∠CDA 的最大值,此最大值即为所求.解答:
 解:∵|
解:∵| -
- |=|
|=| |=λ|
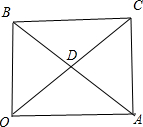
|=λ| |,λ≥2,如图所示:设
|,λ≥2,如图所示:设 =
= ,
, =
= ,OACB为平行四边形,
,OACB为平行四边形,则
 =
= ,
, =
= .
.设|
 |=1,则|
|=1,则| -
- |=|
|=| |=λ,即OC=AB=λ,故平行四边形OACB为矩形,
|=λ,即OC=AB=λ,故平行四边形OACB为矩形, .
.由勾股定理可得OB2+OA2=AB2,即 1+OA2=λ2,∴OA=
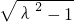 .
.由题意可得,
 与
与 的夹角即∠CDA,由余弦定理CA2=CD2+DA2-2CD•DA•cos∠CDA,
的夹角即∠CDA,由余弦定理CA2=CD2+DA2-2CD•DA•cos∠CDA,即 1=
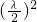 +
+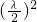 -2×
-2× ×
× ×cos∠CDA∴cos∠CDA=
×cos∠CDA∴cos∠CDA=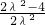 =1-
=1- .
.由于λ≥2,∴1-
 ≥1-
≥1- =
= ,当且仅当λ=2时,取等号,故cos∠CDA 的最小值为
,当且仅当λ=2时,取等号,故cos∠CDA 的最小值为 ,
,故∠CDA 的最大值为
 ,
,故答案为
 .
.点评:本题主要考查两个向量的加减法的法则,以及其几何意义,余弦定理的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )·
)·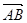 与
与 满足(
满足(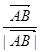 +
+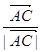 )·
)· =0,且
=0,且
 、
、 满足
满足 ,那么向量
,那么向量 与向量
与向量 的夹角为
的夹角为 B.
B. C.
C. D.
D.
 和
和 满足
满足 ,且
,且 ,
,