Question

已知抛物线y²=8x与椭圆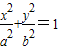有公共焦点F，且椭圆过点D（-）．
（1）求椭圆方程；
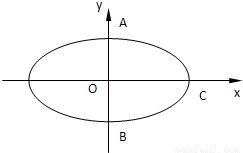
（2）点A、B是椭圆的上下顶点，点C为右顶点，记过点A、B、C的圆为⊙M，过点D作⊙M的切线l，求直线l的方程；
（3）过点A作互相垂直的两条直线分别交椭圆于点P、Q，则直线PQ是否经过定点，若是，求出该点坐标，若不经过，说明理由．

Answer 1

【答案】分析：（1）根据抛物线y²=8x与椭圆有公共焦点F，确定c=2，利用椭圆过点D（-），代入椭圆方程，求出a，b，即可求椭圆方程；
（2）确定⊙M的方程，分类讨论，利用圆心到直线的距离等于半径，即可求得直线l的方程；
（3）设AP、AQ的方程代入椭圆方程，求得P，Q的坐标，可得直线PQ的方程，令x=0，即可得到直线PQ过定点．
解答：解：（1）抛物线y²=8x的焦点F（2，0），
∵抛物线y²=8x与椭圆有公共焦点F，∴c=2，
又椭圆过点D（-），∴，得a²=8，b²=4
∴所求椭圆方程为；
（2）由题意，A（0，2），B（0，-2），C（2，0），则
设M（m，0），由|MA|=|MC|，可得m²+4=（-m）²，∴m=，m²+4=，
∴⊙M：（x-）²+y²=
直线l斜率不存在时，x=-
直线l斜率存在时，设为y-=k（x+）
∴d==，解得k=-
∴直线l为x=-或x+12y-10=0；
（3）显然，两直线斜率存在，设AP：y=k′x+2
代入椭圆方程，得（1+2k′²）x²+8k′x=0，解得x=或x=0
∴点P（，）
同理得Q（，）
直线PQ：y-=（x-）             
令x=0，得y=-=-，
∴直线PQ过定点（0，-）．
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查直线恒过定点，属于中档题．