题目内容
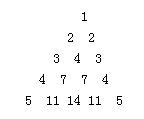
 如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=
如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=an-1+(n-1)
an-1+(n-1)
,由此通过有关求解可以求得:| a2011-2 | 2009 |
1006
1006
(用数字填写)分析:由图表设第n(n>1)行第2个数为an,a2=2,a3=4,a4=7,a5=11…,n≥2,则an=an-1+(n-1),n≥2.由此能导出an=
+1.故a2011=
+1=2021056,由此能求出
的值.
| n(n-1) |
| 2 |
| 2011×2010 |
| 2 |
| a2011-2 |
| 2009 |
解答:解:由图表设第n(n>1)行第2个数为an,
∵a2=2,a3=4,a4=7,a5=11…,
∴n≥2,则an=an-1+(n-1),n≥2.
∵a2=1+1,
a3=1+1+2,
a4=1+1+2+3,
a5=1+1+2+3+4,
an=1+
(1+n-1)(n-1)=
+1.
∴a2011=
+1=2021056,
∴
=
=1006.
故答案为:an-1+(n-1),1006.
∵a2=2,a3=4,a4=7,a5=11…,
∴n≥2,则an=an-1+(n-1),n≥2.
∵a2=1+1,
a3=1+1+2,
a4=1+1+2+3,
a5=1+1+2+3+4,
an=1+
| 1 |
| 2 |
| n(n-1) |
| 2 |
∴a2011=
| 2011×2010 |
| 2 |
∴
| a2011-2 |
| 2009 |
| 2021056-2 |
| 2009 |
故答案为:an-1+(n-1),1006.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化,合理地利用数列的递推公式进行解题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
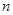 行首尾两数均为
行首尾两数均为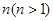 行第2个数为
行第2个数为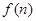 .根据表中上下两行数据关系,可以求得当
.根据表中上下两行数据关系,可以求得当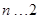 时,
时,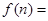 .
.
 如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=________,由此通过有关求解可以求得:
如图数表满足:(1)第n(n>1)行首尾两数均为n,第一行为一个数1;(2)表中的递推关系:从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和.现记第n(n>1)行第2个数为an,如a2=2,a3=4,a4=7,a5=11…,则可以得到递推关系:an=________,由此通过有关求解可以求得: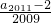 =________(用数字填写)
=________(用数字填写)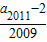 = (用数字填写)
= (用数字填写)
 如图,数表满足;(1)第
如图,数表满足;(1)第