题目内容
如果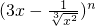 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中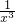 的系数是
的系数是
- A.7
- B.-7
- C.21
- D.-21
C
分析:给二项式中的x赋值-1,求出展开式的各项系数和,列出方程,求出n;将n的值代入二项式,利用二项展开式的通项公式求出通项,令x的指数为-3,求出r的值,将r的值代入通项,求出展开式中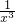 的系数.
的系数.
解答:令x=1得展开式的各项系数之和2n,
∴2n=128,
解得n=7.
∴ 展开式的通项为
展开式的通项为
 ,
,
令 ,
,
解得r=6.
所以展开式中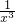 的系数是3C76=21.
的系数是3C76=21.
故选C
点评:本题考查通过给二项式中的x赋值求展开式的系数和、考查利用二项展开式的通项公式解决二项展开式的特定项问题.
分析:给二项式中的x赋值-1,求出展开式的各项系数和,列出方程,求出n;将n的值代入二项式,利用二项展开式的通项公式求出通项,令x的指数为-3,求出r的值,将r的值代入通项,求出展开式中
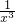 的系数.
的系数.解答:令x=1得展开式的各项系数之和2n,
∴2n=128,
解得n=7.
∴
 展开式的通项为
展开式的通项为 ,
,令
 ,
,解得r=6.
所以展开式中
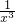 的系数是3C76=21.
的系数是3C76=21.故选C
点评:本题考查通过给二项式中的x赋值求展开式的系数和、考查利用二项展开式的通项公式解决二项展开式的特定项问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中 的系
的系