题目内容
圆x2+y2-4x=0在点P（1，
）处的切线方程为________．
x-y+2=0
分析：求出圆的圆心坐标，求出切点与圆心连线的斜率，然后求出切线的斜率，解出切线方程．
解答：圆x2+y2-4x=0的圆心坐标是（2，0），
所以切点与圆心连线的斜率：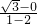
=-，
所以切线的斜率为：
，
切线方程为：y-=（x-1），
即x-y+2=0．
故答案为：x-y+2=0．
点评：本题是基础题，考查圆的切线方程的求法，求出切线的斜率解题的关键，考查计算能力．
y+2=0分析：求出圆的圆心坐标，求出切点与圆心连线的斜率，然后求出切线的斜率，解出切线方程．
解答：圆x2+y2-4x=0的圆心坐标是（2，0），
所以切点与圆心连线的斜率：
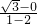=-，所以切线的斜率为：
，切线方程为：y-
=（x-1），即x-
y+2=0．故答案为：x-
y+2=0．点评：本题是基础题，考查圆的切线方程的求法，求出切线的斜率解题的关键，考查计算能力．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
圆x2+y2-4x+4y+6=0截直线x-y-5=0所得的弦长等于（ ）
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、5 |