题目内容
（本小题满分12分）
设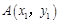
， 
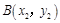两点在抛物线
上，
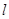是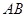
的垂直平分线.
（1）当且仅当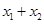
取何值时，直线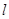经过抛物线的焦点
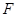？证明你的结论；
（2）当直线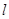的斜率为2时，求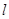在
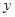轴上截距的取值范围.
【答案】
解：（1）
两点到抛物线的准线的距离相等，
∵抛物线的准线是
轴的平行线，
，依题意
不同时为0．
∴上述条件等价于
∵
，∴上述条件等价于
．
即当且仅当时，
经过抛物线的焦点
.…………………………………6分
（2）设在
轴上的截距为
，依题意得的方程为
；过点
的直线方程可写为
，所以
满足方程
, ∴
.
为抛物线上不同的两点等价于上述方程的判别式
，即
.
设
的中点
的坐标为
，则
，
.
由点在上,
得
，于是
.
故即得在轴上截距的取值范围为
.………………………………12分
【解析】略
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
