题目内容
设x≥0,y≥0且x+2y=
,求函数S=log
(8xy+4y2+1)的最值.
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据已知中x≥0,y≥0且x+2y=
,利用代入消元法,可将函数S=log
(8xy+4y2+1)的真数部分化为-12y2+4y+1(0≤y≤
),结合二次函数的图象和性质,分析真数部分的最值,进而结合对数函数的单调性,可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:∵x≥0,y≥0且x+2y=
,
∴x=-2y+
,(0≤y≤
)
令t=8xy+4y2+1=8(-2y+
)y+4y2+1=-12y2+4y+1,0≤y≤
则当y=
时,t取最大值
,此时函数S取最小值log
;
则当y=0时,t取最小值1,此时函数S取最小值log
1=0;
| 1 |
| 2 |
∴x=-2y+
| 1 |
| 2 |
| 1 |
| 4 |
令t=8xy+4y2+1=8(-2y+
| 1 |
| 2 |
| 1 |
| 4 |
则当y=
| 1 |
| 6 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
则当y=0时,t取最小值1,此时函数S取最小值log
| 1 |
| 2 |
点评:本题考查的知识点是对数函数的图象与性质,二次函数的图象和性质,其中熟练掌握二次函数的图象和性质及对数函数的图象和性质是解答的关键.

练习册系列答案
相关题目
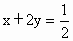 ,求函数
,求函数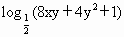 的最大值与最小值.
的最大值与最小值.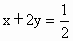 ,求函数
,求函数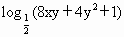 的最大值与最小值.
的最大值与最小值.