题目内容
 (文科)如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.
(文科)如图,已知PA与圆O相切于点A,半径OB⊥OP,AB交PO于点C.(Ⅰ)求证:PA=PC;
(Ⅱ)若圆O的半径为3,OP=5,求BC的长度.
分析:(I)根据弦切角定理,可得∠PAB=∠ACB,根据圆周角定理可得∠BAC=90°,结合BC⊥OP,根据同角的余角相等及对顶角相等可得∠PDA=∠PAB,即△PAD为等腰三角形
(II)先求出∠AOP,在等腰三角形AOB中,求出∠OBC,利用Rt△BOC中,BC=
,求出答案.
(II)先求出∠AOP,在等腰三角形AOB中,求出∠OBC,利用Rt△BOC中,BC=
| OB |
| cos∠OBC |
解答: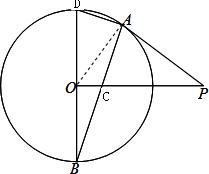 证明:(I)∵PA与圆O相切于点A,
证明:(I)∵PA与圆O相切于点A,
∴∠PAB=∠ADB
∵BD为圆O的直径,
∴∠BAD=90°
∴∠ADB=90°-∠B
∵BD⊥OP,
∴∠BCO=90°-∠B
∴∠BCO=∠PCA=∠PAB
即△PAC为等腰三角形
∴PA=PC;
(Ⅱ)解:由题意得 Rt△AOP中,cos∠AOP=
=
,cos
=
,sin
=
;
∴∠AOB=
+∠AOP,
∴等腰三角形AOB中,∠OBC=
=
-
,
由和差角公式得:cos∠OBC=
.
在Rt△BOC中,BC=
=
=
.
 证明:(I)∵PA与圆O相切于点A,
证明:(I)∵PA与圆O相切于点A,∴∠PAB=∠ADB
∵BD为圆O的直径,
∴∠BAD=90°
∴∠ADB=90°-∠B
∵BD⊥OP,
∴∠BCO=90°-∠B
∴∠BCO=∠PCA=∠PAB
即△PAC为等腰三角形
∴PA=PC;
(Ⅱ)解:由题意得 Rt△AOP中,cos∠AOP=
| OA |
| OP |
| 3 |
| 5 |
| ∠AOP |
| 2 |
2
| ||
| 5 |
| ∠AOP |
| 2 |
| ||
| 5 |
∴∠AOB=
| π |
| 2 |
∴等腰三角形AOB中,∠OBC=
π-(
| ||
| 2 |
| π |
| 4 |
| ∠AOP |
| 2 |
由和差角公式得:cos∠OBC=
3
| ||
| 10 |
在Rt△BOC中,BC=
| OB |
| cos∠OBC |
| 3 | ||||
|
| 10 |
点评:本题考查的知识点是弦切角定理,圆周角定理,等腰三角形的判定,相似三角形的判定与性质,难度不大,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q.
(2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q. 如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).
如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).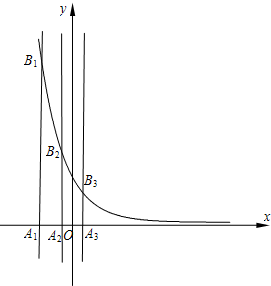 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数
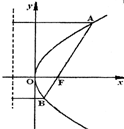 如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).
如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2). ;
; 时,求弦长|AB|.
时,求弦长|AB|.