题目内容
给定命题p:函数 和函数
和函数 的图象关于原点对称;命题q:当
的图象关于原点对称;命题q:当 (k∈Z)时,函数
(k∈Z)时,函数 取得极小值.下列说法正确的是( )
取得极小值.下列说法正确的是( )A.p∨q是假命题
B.¬p∧q是假命题
C.p∧q是真命题
D.¬p∨q是真命题
【答案】分析:根据函数图象的对称变换及诱导公式,对两个函数的解析式变形,可判断命题p为真命题;根据和差角公式,将函数的解析式化为正弦型函数,再根据正弦型函数的图象和性质,可判断命题q为假命题.再由复合命题真假判断的真值表可得答案.
解答:解:函数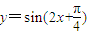 的图象关于原点对称的函数解析式为
的图象关于原点对称的函数解析式为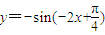 =
=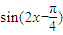 ,函数
,函数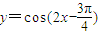 =
=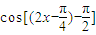 =
=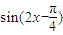 ,故命题p为真命题;
,故命题p为真命题;
函数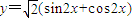 =2
=2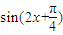 ,当
,当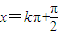 (k∈Z)时,相位角的终边未落在y轴非正半轴上,故此时不取极小值,故命题q为假命题;
(k∈Z)时,相位角的终边未落在y轴非正半轴上,故此时不取极小值,故命题q为假命题;
故p∨q是真命题,¬p∧q是假命题,p∧q是假命题,¬p∨q是假命题
故选B
点评:本题考查的知识点是复合命题的真假,三角函数的图象和性质,熟练掌握三角函数的图象和性质是解答的关键.
解答:解:函数
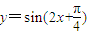 的图象关于原点对称的函数解析式为
的图象关于原点对称的函数解析式为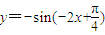 =
=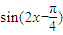 ,函数
,函数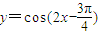 =
=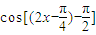 =
=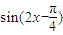 ,故命题p为真命题;
,故命题p为真命题;函数
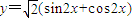 =2
=2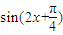 ,当
,当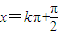 (k∈Z)时,相位角的终边未落在y轴非正半轴上,故此时不取极小值,故命题q为假命题;
(k∈Z)时,相位角的终边未落在y轴非正半轴上,故此时不取极小值,故命题q为假命题;故p∨q是真命题,¬p∧q是假命题,p∧q是假命题,¬p∨q是假命题
故选B
点评:本题考查的知识点是复合命题的真假,三角函数的图象和性质,熟练掌握三角函数的图象和性质是解答的关键.

练习册系列答案
相关题目