题目内容
函数y=
x-2+4cos2
在区间[0，
]上的最大值是
+1
+1．
| 3 |
| x |
| 2 |
| π |
| 2 |
| ||
| 3 |
| ||
| 3 |
分析：把函数解析式利用二倍角的余弦函数公式化简，利用求导法则求出导函数，令导函数值为0求出x的值，利用x的值分区间讨论导函数的正负，可得出函数的单调区间，由函数的单调性可得函数的最大值．
解答：解：∵y=
x-2+4cos2
=
x-2+2（1+cosx）
=
x+2cosx，
∴y′=
-2sinx，
令y′=0，解得sinx=
，又x∈[0，
]，∴x=
，
当0＜x＜
时，y′＞0，函数为增函数；
当
≤x＜
时，y′＜0，函数为减函数，
则当x=
时，函数取最大值，最大值为yx=
=
+1．
故答案为：
+1
| 3 |
| x |
| 2 |
=
| 3 |
=
| 3 |
∴y′=
| 3 |
令y′=0，解得sinx=
| ||
| 2 |
| π |
| 2 |
| π |
| 3 |
当0＜x＜
| π |
| 3 |
当
| π |
| 3 |
| π |
| 2 |
则当x=
| π |
| 3 |
| π |
| 3 |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：此题考查了二倍角的余弦函数公式，求导法则，利用导数研究函数的单调性，以及利用导数求函数的最值，熟练运用三角函数的恒等变形把函数解析式化简是本题的突破点，解题的关键是利用导函数的正负得出函数的单调性．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
已知函数y=3x-4的值域为[-10，5]，则它的定义域是（ ）
| A、[-2，3] | B、[-1，4] | C、[-2，2] | D、[-1，3] |
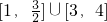，则区间[m，n]可以是________．（把你认为正确的序号都填上）