题目内容
已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:![]()
![]() .
.
解:(1)![]() 的定义域为(0,+∞),
的定义域为(0,+∞),![]()
当![]() 时,
时,![]() >0,故
>0,故![]() 在(0,+∞)单调递增;
在(0,+∞)单调递增;
当![]() 时,
时,![]() <0,故
<0,故![]() 在(0,+∞)单调递减;
在(0,+∞)单调递减;
当-1<![]() <0时,令
<0时,令![]() =0,解得
=0,解得![]() .
.
则当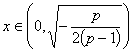 时,
时,![]() >0;
>0;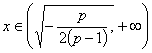 时,
时,![]() <0.
<0.
故![]() 在
在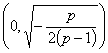 单调递增,在
单调递增,在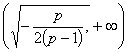 单调递减
单调递减
(2)因为![]() ,所以
,所以
当![]() 时,
时,![]() 恒成立
恒成立![]()
令![]() ,则
,则![]() ,
,
因为![]() ,由
,由![]() 得
得![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减.所以
上递减.所以![]() ,故
,故![]()
(3)由(2)知当![]() 时,有
时,有![]() ,当
,当![]() 时,
时,![]() 即
即![]() ,
,
令![]() ,则
,则![]() ,即
,即![]()
所以![]() ,
,![]() ,…,
,…,![]() ,
,
相加得![]()
而![]()
所以![]() ,
,![]()

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知函数f(x)=
+
的定义域是( )
| 1-x2 |
| x2-1 |
| A、[-1,1] |
| B、{-1,1} |
| C、(-1,1) |
| D、(-∞,-1]∪[1,+∞) |