题目内容
已知函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0)的图像在y轴右侧的第一个最高点(函数取最大值的点)为M(2,2
活动:本例是一道经典例题,主要考查三角函数模型的应用,及训练学生分析思维能力,对数形结合的思维要求也较高.教师可引导学生展开思考讨论,怎样根据题目中给出的条件找到思维的切入点.题目中虽然没有直接给出图像,实质是已知图像求解析式问题.指导学生画出草图,利用数形结合来深化题意的理解,事实上,学生很容易看出A的值.如果学生没找出周期,教师可进一步点拨:题目中告诉的x轴的横坐标2与6表示图像的哪段.根据题意,知道点M、N恰是函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0)在对应于包含0的周期的那段图像的五个关键点中的两个.由此可知A、T.但要注意指导φ的求法.
解:方法一:
根据题意,可知![]() =6-2=4,所以T=16.于是ω=
=6-2=4,所以T=16.于是ω=![]() =
=![]() .
.
将点M的坐标(2,2![]() )代入y=2
)代入y=2![]() sin(
sin(![]() x+φ),
x+φ),
得2![]() =2
=2![]() sin(
sin(![]() ×2+φ),即sin(
×2+φ),即sin(![]() +φ)=1.
+φ)=1.
所以满足![]() +φ=
+φ=![]() 的φ为最小正数解为φ=
的φ为最小正数解为φ=![]() .
.
从而所求的函数解析式是y=2![]() sin(
sin(![]() x+
x+![]() ),x∈R.
),x∈R.
方法二:将两个点M(2,2![]() ),N(6,0)的坐标分别代入y=2
),N(6,0)的坐标分别代入y=2![]() sin(ωx+φ)并化简,
sin(ωx+φ)并化简,
得![]()
所以,在长度为一个周期且包含原点的闭区间上,有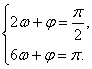 .
.
从而所求的函数解析式是y=2![]() sin(
sin(![]() x+
x+![]() ),x∈R.
),x∈R.
点评:由三角函数图像求解析式确定φ时,答案可能止一个,这里可提醒学生注意,习惯上一般取离x轴最近的一个,这样的解析式简洁.本例对学生有着很高的训练价值,特别是数形结合思想、转化与化归思想的运用.数形结合是数学中重要的思想方法,对各类函数的研究都离不开图像,在中学阶段,几乎所有函数的性质都是通过观察图像而得到的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数y=Asin(ωx+φ),在同一周期内,当x=
时,取最大值y=2,当x=
时,取得最小值y=-2,那么函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
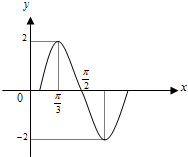 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A、y=2sin(
| ||||
B、y=2sin(3x+
| ||||
C、y=2sin(3x-
| ||||
D、y=2sin(3x-
|
 已知函数
已知函数 已知函数
已知函数