题目内容
设函数f(x)=x3+ax2+bx(x>0)的图象与直线y=4相切于M(1,4).
(Ⅰ)求f(x)=x3+ax2+bx在区间(0,4]上的最大值与最小值;
(Ⅱ)设存在两个不等正数s,t(s<t),当x∈[s,t]时,函数f(x)=x3+ax2+bx的值域是[ks,kt],求正数k的取值范围.
解析:
(Ⅰ)![]() (x)=3x2+2ax+b.依题意则有:
(x)=3x2+2ax+b.依题意则有:
![]() 所以
所以![]() 解得
解得![]() 所以f(x)=x3-6x2+9x;
所以f(x)=x3-6x2+9x;
![]() (x)=3x2-12x+9=3(x-1)(x-3),由
(x)=3x2-12x+9=3(x-1)(x-3),由![]() (x)=0可得x=1或x=3.
(x)=0可得x=1或x=3.
![]() (x),f(x)在区间(0,4]上的变化情况为:
(x),f(x)在区间(0,4]上的变化情况为:
所以函数f(x)=x3-6x2+9x在区间[0,4]上的最大值是4,最小值是0.
(2)由函数的定义域是正数知,s>0,故极值点(3,0)不在区间[s,t]上;
①若极值点M(1,4)在区间[s,t]上,此时0<s≤1≤t<3,
故有(i) 或(ii)
或(ii)
(i)由k=![]() ,1≤t<3知,k∈
,1≤t<3知,k∈![]() ,当且仅当t=1时,k=4;
,当且仅当t=1时,k=4;
再由k=(s-3)2,0<s≤1知,k∈[4,9),当且仅当s=1时,k=4.
由于s≠t,故不存在满足要求的k值.
(ii)由s=![]() f(t)=
f(t)=![]() f(t)=
f(t)=![]() ,及0<s≤1可解得2≤t<3,
,及0<s≤1可解得2≤t<3,
所以k=![]() ,2≤t<3知,k∈
,2≤t<3知,k∈![]() ;
;
即当k∈![]() 时,存在t=
时,存在t=![]() ∈[2,3),s=
∈[2,3),s=![]() f(t)=
f(t)=![]() ∈(0,1],且f(s)≥4s=
∈(0,1],且f(s)≥4s=![]() f(t)>f(t),满足要求.
f(t)>f(t),满足要求.
②若函数f(x)在区间[s,t]上单调递增,则0<s<t≤1或3<s<t,
且![]() ,故s,t是方程x2-6x+9=k的两根,
,故s,t是方程x2-6x+9=k的两根,
由于此方程两根之和为3,故[s,t]不可能同在一个单调增区间内;
③若函数f(x)在区间[s,t]上单调递减,则1<s<t<3,![]() ,
,
两式相减并整理得s2(s-3)3=t2(t-3)2,由1<s<t<3知s(s-3)=t(t-3),即s+t=3,
再将两式相减并除以s-t得
-k=(s2+st+t2)-6(s+t)+9=(s+t)2-6(s+t)+9-st=-st,
即k=st,所以s,t是方程x2-3x+k=0的两根,
令g(x)=x2-3x+k,
则 ,即存在s=
,即存在s=![]() 满足要求.
满足要求.
综上可得,当![]() <k<
<k<![]() 时,存在两个不等正数s,t(s<t),使x∈[s,t]时,函数f(x)=x3-6x2+9x的值域恰好是[ks,kt].
时,存在两个不等正数s,t(s<t),使x∈[s,t]时,函数f(x)=x3-6x2+9x的值域恰好是[ks,kt].

 x3-
x3- x2+a x.
x2+a x.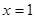 处的切线方程为12x+y-1=0.
处的切线方程为12x+y-1=0. 上的最大值和最小值.
上的最大值和最小值.