题目内容
已知函数f(x)=|ax-2|+blnx(x>0,实数a,b为常数).(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程
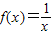 在(0,1]上解的个数.
在(0,1]上解的个数.
【答案】分析:(1)先去掉绝对值转化为分段函数,每一段用导数法研究,因为是增函数,则导数大于等于零恒成立,最后每一段的结果取交集.
(2)先构造g(x)=|ax-2|+lnx-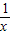 ,即g(x)=
,即g(x)=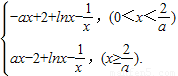 ,每一段再用导数法研究.
,每一段再用导数法研究.
解答:解:(1)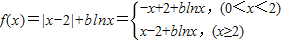
①当0<x<2时,f(x)=-x+2+blnx,f′(x)=-1+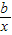 .
.
由条件,得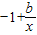 ≥0恒成立,即b≥x恒成立.
≥0恒成立,即b≥x恒成立.
∴b≥2
②当x≥2时,f(x)=x-2+blnx,f'(x)=1+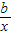 .
.
由条件,得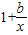 ≥0恒成立,即b≥-x恒成立
≥0恒成立,即b≥-x恒成立
∴b≥-2
∵f(x)的图象在(0,+∞)不间断,
综合①,②得b的取值范围是b≥2.
(2)令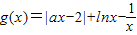 ,即
,即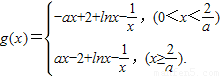
当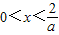 时,
时,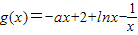 ,
,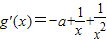 ,
,
∵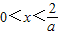 ,∴
,∴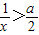 ,则
,则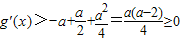
即g'(x)>0,∴g(x)在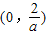 上是单调增函数.
上是单调增函数.
当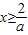 时,
时,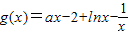 ,
,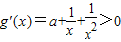
∴g(x)在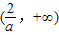 上是单调增函数.
上是单调增函数.
∵g(x)的图象在(0,+∞)上不间断,
∴g(x)在(0,+∞)上是单调增函数.
∵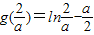 ,而a≥2,∴
,而a≥2,∴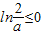 ,则
,则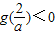 .g(1)=|a-2|-1=a-3
.g(1)=|a-2|-1=a-3
①当a≥3时,
∵g(1)≥0
,∴g(x)=0在(0,1]上有惟一解.
即方程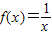 解的个数为1个.
解的个数为1个.
②当2≤a<3时,
∵g(1)<0,
∴g(x)=0在(0,1]上无解.
即方程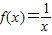 解的个数为0个.
解的个数为0个.
点评:本题主要考查函数的单调性与最值,一般来讲,给出解析式的,解决的方法往往是基本函数法或导数法,抽象函数的单调性和最值,往往用单调性的定义解决.
(2)先构造g(x)=|ax-2|+lnx-
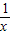 ,即g(x)=
,即g(x)=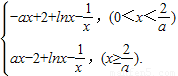 ,每一段再用导数法研究.
,每一段再用导数法研究.解答:解:(1)
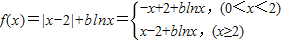
①当0<x<2时,f(x)=-x+2+blnx,f′(x)=-1+
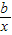 .
.由条件,得
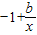 ≥0恒成立,即b≥x恒成立.
≥0恒成立,即b≥x恒成立.∴b≥2
②当x≥2时,f(x)=x-2+blnx,f'(x)=1+
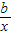 .
.由条件,得
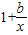 ≥0恒成立,即b≥-x恒成立
≥0恒成立,即b≥-x恒成立∴b≥-2
∵f(x)的图象在(0,+∞)不间断,
综合①,②得b的取值范围是b≥2.
(2)令
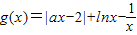 ,即
,即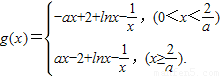
当
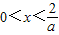 时,
时,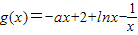 ,
,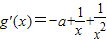 ,
,∵
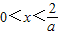 ,∴
,∴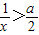 ,则
,则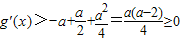
即g'(x)>0,∴g(x)在
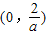 上是单调增函数.
上是单调增函数.当
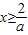 时,
时,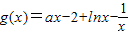 ,
,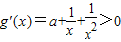
∴g(x)在
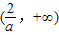 上是单调增函数.
上是单调增函数.∵g(x)的图象在(0,+∞)上不间断,
∴g(x)在(0,+∞)上是单调增函数.
∵
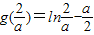 ,而a≥2,∴
,而a≥2,∴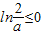 ,则
,则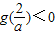 .g(1)=|a-2|-1=a-3
.g(1)=|a-2|-1=a-3①当a≥3时,
∵g(1)≥0
,∴g(x)=0在(0,1]上有惟一解.
即方程
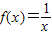 解的个数为1个.
解的个数为1个.②当2≤a<3时,
∵g(1)<0,
∴g(x)=0在(0,1]上无解.
即方程
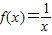 解的个数为0个.
解的个数为0个.点评:本题主要考查函数的单调性与最值,一般来讲,给出解析式的,解决的方法往往是基本函数法或导数法,抽象函数的单调性和最值,往往用单调性的定义解决.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|