题目内容
11.如图所示的四棱锥P-ABCD,底面四边形ABCD中,AD=BC=$\sqrt{5}$,AB=2CD=2$\sqrt{2}$,BO=2DO=2,PO⊥底面ABCD,且PA⊥PC.(1)求VP-ABCD;
(2)求面PAD与面PBC所成的锐二面角的余弦值.

分析 (1)由题意求出高PO,然后求解几何体的体积.
(2)建立空间直角坐标系,求出相关点的坐标,求出平面PAD与平面PBC的法向量,即可求解面PAD与面PBC所成的锐二面角的余弦值.
解答  解:(1)连结OC,OA,∵AD=BC=$\sqrt{5}$,AB=2CD=2$\sqrt{2}$,BO=2DO=2,∴BD⊥OC,BD⊥OA,AOC在同一直线上,并且OC=1,OA=2,如图:
解:(1)连结OC,OA,∵AD=BC=$\sqrt{5}$,AB=2CD=2$\sqrt{2}$,BO=2DO=2,∴BD⊥OC,BD⊥OA,AOC在同一直线上,并且OC=1,OA=2,如图:
PO⊥底面ABCD,且PA⊥PC.
可得PC2=PO2+1,PA2=PO2+4,PC2+PA2=9,
可得2PO2+5=9,∴PO=2.
VP-ABCD=$\frac{1}{3}{S}_{ABCD}•PO$=$\frac{1}{3}×\frac{1}{2}×3×(1+2)×2$
=3.
(2)以O为坐标原点,OA,OB,OP为坐标轴,建立如图空间直角坐标系,如图:
则O(0,0,0),A(2,0,0),B(0,2,0),C(-1,0,0),D(0,-1,0),P(0,0,2).
平面PAD的法向量为$\overrightarrow{m}$=(x,y,z),可得$\left\{\begin{array}{l}\overrightarrow{m}•\overrightarrow{AD}=0\\ \overrightarrow{m}•\overrightarrow{DP}=0\end{array}\right.$,
即$\left\{\begin{array}{l}-2x-y=0\\ y+2z=0\end{array}\right.$,令y=2,则x=-1,z=-1,$\overrightarrow{m}$=(-1,2,-1),
平面PBC的法向量为$\overrightarrow{n}$=(x,y,z),可得$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{BC}=0\\ \overrightarrow{n}•\overrightarrow{CP}=0\end{array}\right.$,
即$\left\{\begin{array}{l}x+2z=0\\-x-2y=0\end{array}\right.$,令x=2,则y=-1,z=-1,$\overrightarrow{n}$=(2,-1,-1),
面PAD与面PBC所成的锐二面角的余弦值:cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{\left|\overrightarrow{m}\right|\left|\overrightarrow{n}\right|}$=$\frac{3}{6}$=$\frac{1}{2}$
点评 本题考查几何体的体积的求法,二面角的平面角的解法,考查空间想象能力以及计算能力.

| A. | $[{\frac{1}{2},1}]$ | B. | $[{\frac{3}{4},1}]$ | C. | $[{\frac{1}{2},\frac{3}{4}}]$ | D. | $[{\frac{3}{8},\frac{3}{4}}]$ |
 矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF展开后再折成如图所示,使点A落在EF上的点A′处,求第二次折痕BG的长.
矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF展开后再折成如图所示,使点A落在EF上的点A′处,求第二次折痕BG的长.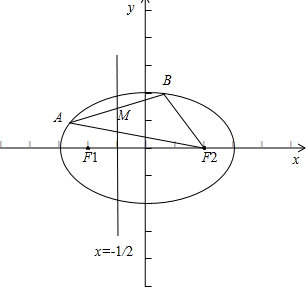 如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.
如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.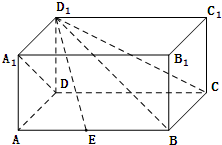 在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1.
在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1.