Question

【题目】长方体ABCD－A1B1C1D1中，AA1＝AB＝2，AD＝1，点E、F、G分别是DD1、AB、CC1的中点．求异面直线A1E与GF所成角的大小．

Answer 1

【答案】90°

【解析】

连接B1G，EG，B1F，CF，证明∠B1GF(或其补角)就是异面直线A1E与GF所成的角，再解三角形求出∠B1GF＝90°.

连接B1G，EG，B1F，CF.

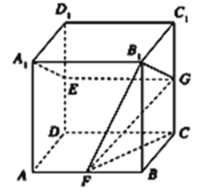
∵E、G是棱DD1、CC1的中点，

∴A1B1∥EG，A1B1=EG.

∴四边形A1B1GE是平行四边形．

∴B1G∥A1E.

∴∠B1GF(或其补角)就是异面直线A1E与GF所成的角．

在Rt△B1C1G中，B1C1＝AD＝1，C1G＝AA1＝1，

∴B1G＝.

在Rt△FBC中，BC＝BF＝1，

∴FC＝.

在Rt△FCG中，CF＝，CG＝1，

∴FG＝.

在Rt△B1BF中，BF＝1，B1B＝2，

∴B1F＝，在△B1FG中，B1G2＋FG2＝B1F2，

∴∠B1GF＝90°.

因此异面直线A1E与GF所成的角为90°.