题目内容
（2011•丰台区一模）已知函数f（x）=
，若则实数x的取值范围是（ ）
|
分析：观察发现，函数f（x）=
，在R上是增函数，则不等式易解，本题要先判断函数的单调性，再解不等式．
|
解答：解：当x≤0时，f（x）=x3，是增函数，且f（x）≤f（0）=0
当x＞0时，f（x）=ln（x+1），是增函数，且f（x）＞f（0）=0
故函数在R上是增函数，
∵f（2-x2）＞f（x），
∴2-x2＞x，解得-2＜x＜1
故实数x的取值范围为（-2，1）．
故选D
当x＞0时，f（x）=ln（x+1），是增函数，且f（x）＞f（0）=0
故函数在R上是增函数，
∵f（2-x2）＞f（x），
∴2-x2＞x，解得-2＜x＜1
故实数x的取值范围为（-2，1）．
故选D
点评：此题考查了其他不等式的解法，考查了分类讨论的数学思想，是一道基础题．
练习册系列答案
相关题目
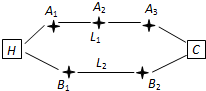（2011•丰台区二模）张先生家住H小区，他在C科技园区工作，从家开车到公司上班有L1，L2两条路线（如图），L1路线上有A1，A2，A3三个路口，各路口遇到红灯的概率均为