题目内容
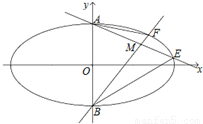
已知椭圆C: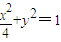 的短轴的端点分别为A,B,直线AM,BM分别与椭圆C交于E,F两点,其中点M (m,
的短轴的端点分别为A,B,直线AM,BM分别与椭圆C交于E,F两点,其中点M (m, ) 满足m≠0,且
) 满足m≠0,且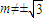 .
.(Ⅰ)求椭圆C的离心率e;
(Ⅱ)用m表示点E,F的坐标;
(Ⅲ)若△BME面积是△AMF面积的5倍,求m的值.
【答案】分析:(Ⅰ)利用椭圆的离心率计算公式 ;
;
(Ⅱ)利用点斜式分别写出直线AM、BM的方程,与椭圆的方程联立即可得到点E、F的坐标;
(Ⅲ)利用三角形的面积公式及其关系得到 ,再利用坐标表示出即可得到m的值.
,再利用坐标表示出即可得到m的值.
解答:解:(Ⅰ)依题意知a=2, ,∴
,∴ ;
;
(Ⅱ)∵A(0,1),B(0,-1),M (m, ),且m≠0,
),且m≠0,
∴直线AM的斜率为k1= ,直线BM斜率为k2=
,直线BM斜率为k2= ,
,
∴直线AM的方程为y= ,直线BM的方程为y=
,直线BM的方程为y= ,
,
由 得(m2+1)x2-4mx=0,
得(m2+1)x2-4mx=0,
∴ ,∴
,∴ ,
,
由 得(9+m2)x2-12mx=0,
得(9+m2)x2-12mx=0,
∴ ,∴
,∴ ;
;
(Ⅲ)∵ ,
, ,∠AMF=∠BME,5S△AMF=S△BME,
,∠AMF=∠BME,5S△AMF=S△BME,
∴5|MA||MF|=|MB||ME|,∴ ,
,
∴ ,
,
∵m≠0,∴整理方程得 ,即(m2-3)(m2-1)=0,
,即(m2-3)(m2-1)=0,
又∵ ,∴m2-3≠0,∴m2=1,∴m=±1为所求.
,∴m2-3≠0,∴m2=1,∴m=±1为所求.
点评:熟练掌握椭圆的离心率、点斜式、直线与椭圆的相交问题的解题模式、三角形的面积计算公式、比例式如何用坐标表示是解题的关键.
 ;
;(Ⅱ)利用点斜式分别写出直线AM、BM的方程,与椭圆的方程联立即可得到点E、F的坐标;
(Ⅲ)利用三角形的面积公式及其关系得到
 ,再利用坐标表示出即可得到m的值.
,再利用坐标表示出即可得到m的值.解答:解:(Ⅰ)依题意知a=2,
 ,∴
,∴ ;
; (Ⅱ)∵A(0,1),B(0,-1),M (m,
 ),且m≠0,
),且m≠0,∴直线AM的斜率为k1=
 ,直线BM斜率为k2=
,直线BM斜率为k2= ,
,∴直线AM的方程为y=
 ,直线BM的方程为y=
,直线BM的方程为y= ,
,由
 得(m2+1)x2-4mx=0,
得(m2+1)x2-4mx=0,∴
 ,∴
,∴ ,
,由
 得(9+m2)x2-12mx=0,
得(9+m2)x2-12mx=0,∴
 ,∴
,∴ ;
; (Ⅲ)∵
 ,
, ,∠AMF=∠BME,5S△AMF=S△BME,
,∠AMF=∠BME,5S△AMF=S△BME,∴5|MA||MF|=|MB||ME|,∴
 ,
,∴
 ,
,∵m≠0,∴整理方程得
 ,即(m2-3)(m2-1)=0,
,即(m2-3)(m2-1)=0,又∵
 ,∴m2-3≠0,∴m2=1,∴m=±1为所求.
,∴m2-3≠0,∴m2=1,∴m=±1为所求.点评:熟练掌握椭圆的离心率、点斜式、直线与椭圆的相交问题的解题模式、三角形的面积计算公式、比例式如何用坐标表示是解题的关键.

练习册系列答案
相关题目
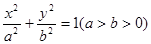 的短轴长为
的短轴长为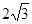 ,右焦点
,右焦点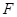 与抛物线
与抛物线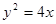 的焦点重合,
的焦点重合, 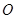 为坐标原点
为坐标原点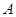 、
、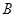 是椭圆C上的不同两点,点
是椭圆C上的不同两点,点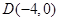 ,且满足
,且满足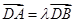 ,若
,若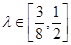 ,求直线AB的斜率的取值范围.
,求直线AB的斜率的取值范围. 的短轴长等于焦距,椭圆C上的点到右焦点F的最短距离为
的短轴长等于焦距,椭圆C上的点到右焦点F的最短距离为 。
。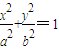 的短轴长等于焦距,椭圆C上的点到右焦点F的最短距离为
的短轴长等于焦距,椭圆C上的点到右焦点F的最短距离为 .
.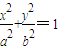 的短轴长等于焦距,椭圆C上的点到右焦点F的最短距离为
的短轴长等于焦距,椭圆C上的点到右焦点F的最短距离为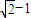 .
.