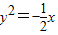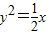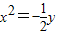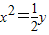题目内容
p={x|x2-4ax+3a2＜0（a＞0）}，
且￢p是￢q的必要不充分条件，求a的取值范围．
|
x2-4ax+3a2=0对应的根为a，3a；由于a＞0，
则x2-4ax+3a2＜0的解集为（a，3a），故命题p成立有x∈（a，3a）；
由x2-x-6≤0得x∈[-2，3]，x2+2x-8＞0得x∈（2，+∞）∪（-∞，-4），
故命题q成立有x∈[-2，+∞）∪（-∞，-4），
若?p是?q的必要不充分条件，即p是q的充分不必要条件，
因此有a＞0满足题意，
故a的取值范围为：a＞0．
则x2-4ax+3a2＜0的解集为（a，3a），故命题p成立有x∈（a，3a）；
由x2-x-6≤0得x∈[-2，3]，x2+2x-8＞0得x∈（2，+∞）∪（-∞，-4），
故命题q成立有x∈[-2，+∞）∪（-∞，-4），
若?p是?q的必要不充分条件，即p是q的充分不必要条件，
因此有a＞0满足题意，
故a的取值范围为：a＞0．
练习册系列答案
相关题目
当a为任意实数时，直线（2a+3）x+y-4a+2=0恒过定点P，则过点P的抛物线的标准方程是（ ）
A、x2=32y或y2=-
| ||
B、x2=-32y或y2=
| ||
C、y2=32x或x2=-
| ||
D、y2=-32x或x2=
|
