题目内容
如图,已知正方体ABCD—A1B1C1D1中,E、F分别是AB和BC的中点,试问在棱DD1上能否找到一点M,使BM⊥平面B1EF?若能,试确定点M的位置;若不能,请说明理由.
思路解析:这是一道探索性问题,可从假设结论成立入手去分析.我们考虑如果BM⊥平面B1EF时,点M应该满足使BM⊥B1E,即其在平面A1B上的射影BP应该满足BP⊥B1E,经计算,不难得到点M应为DD1的中点.
证明:如下图,取DD1的中点M,AA1的中点P,CC1的中点Q.

连结MP、MQ、BP、BQ,易证得MP⊥面ABB1A1,
∴MP⊥B1E.
又由平面几何知BP⊥B1E,∴B1E⊥平面MBP.
∴B1E⊥MB.
同理可得BM⊥B1F.
又B1E∩B1F=B1,∴BM⊥平面B1EF.
方法归纳 在空间几何中证线面垂直常用的方法有:
(1)由线面垂直证线线垂直;(2)由三垂线定理及其逆定理证线线垂直.
巧解提示 由于本题中涉及面的垂线、斜线及斜线在面内的射影,所以可用三垂线定理去证明.
证明:如图,取DD1的中点M,AA1的中点P,CC1的中点Q.
连结MP,MQ,BP,BQ,易证MP⊥面ABB1A1,由平面几何知识知BP⊥B1Q,
∴B1E⊥BM.
同理可得BM⊥B1F.
又∵B1E∩B1F=B,∴BM⊥平面B1EF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )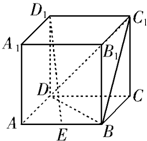 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.