题目内容
已知命题
，命题q：x2+2x+1-m≤0（m＞0）若非p是非q的必要不充分条件，那么实数m的取值范围是________．
[4，+∞）
分析：先求出非p、非q为真时，m的范围，再利用非p是非q的必要不充分条件，可求实数m的取值范围．
解答：由题意，
，∴
或x≥1；
q：x2+2x+1-m≤0（m＞0），∴?q：x2+2x+1-m＞0，∴（x+1）2＞m，
解得
或
∵?p是?g的必要不充分条件，∴
，∴m≥4．
故实数m的取值范围是[4，+∞）
故答案为：[4，+∞）
点评：本题考查不等式的求解，考查四种条件，解题的关键是求出非p、非q为真时，m的范围．
分析：先求出非p、非q为真时，m的范围，再利用非p是非q的必要不充分条件，可求实数m的取值范围．
解答：由题意，
，∴或x≥1；q：x2+2x+1-m≤0（m＞0），∴?q：x2+2x+1-m＞0，∴（x+1）2＞m，
解得
或∵?p是?g的必要不充分条件，∴
，∴m≥4．故实数m的取值范围是[4，+∞）
故答案为：[4，+∞）
点评：本题考查不等式的求解，考查四种条件，解题的关键是求出非p、非q为真时，m的范围．
练习册系列答案
相关题目
，命题q：(x＋a)(x－3)＞0，若p是q的充分不必要条件，则实数a的取值范围是
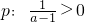；命题q：?x∈R，x2+2ax+2-a=0．若命题“￢p且q”是真命题，求实数a的取值范围．