题目内容
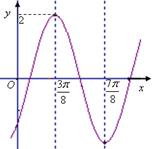已知函数f(x)=2sin(ωx+φ)(ω＞0，-| π |
| 2 |
| π |
| 2 |
| 3π |
| 8 |
| 7π |
| 8 |
（1）求函数f（x）的解析式并写出函数的单调增区间；
（2）若f（α）=
| 6 |
| 5 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 8 |
分析：（1）结合函数的图象，求出A，T，然后求出ω，根据极值点求出φ，确定函数f（x）的解析式，利用正弦函数的单调增区间求出函数的单调增区间；
（2）利用f（α）=
且
＜α＜
，求出sin(2α-
)=
和cos(2α-
)，化简f（α+
），然后求出它的值．
法二：利用f（α）=
且
＜α＜
，求出2sin2α=
，然后化简f（α+
），求出f（α+
）的值．
法三：由sin(2α-
)=
得sin2α-cos2α=
，求出cos4α，再求出2sin2α=
，然后化简f（α+
），求出f（α+
）的值．
（2）利用f（α）=
| 6 |
| 5 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| π |
| 8 |
法二：利用f（α）=
| 6 |
| 5 |
| π |
| 8 |
| 3π |
| 8 |
7
| ||
| 5 |
| π |
| 8 |
| π |
| 8 |
法三：由sin(2α-
| π |
| 4 |
| 3 |
| 5 |
3
| ||
| 5 |
7
| ||
| 5 |
| π |
| 8 |
| π |
| 8 |
解答：解：（1）由题意，
=
-
=
，∴T=π，
又ω＞0，故ω=2，∴f（x）=2sin（2x+φ），（2分）
由f(
)=2sin(
+φ)=2，解得φ=2kπ-
(k∈Z)，
又-
＜φ＜
，∴φ=-
，∴f(x)=2sin(2x-
)．（5分）
由2kπ-
≤2x-
≤2kπ+
(k∈Z)知，kπ-
≤x≤kπ+
(k∈Z)
∴函数f（x）的单调增区间为[kπ-
，kπ+
](k∈Z)．（7分）
（2）解法1：依题意得：2sin(2α-
)=
，即sin(2α-
)=
，（8分）
∵
＜α＜
，∴0＜2α-
＜
，
∴cos(2α-
)=
=
=
，（10分）
f(
+α)=2sin[(2α-
)+
]
∵sin[(2α-
)+
]=sin(2α-
)cos
+cos(2α-
)sin
=
(
+
)=
f(
+α)=
．（14分）
解法2：依题意得：sin(2α-
)=
，sin2α-cos2α=
得，①（9分）
∵
＜α＜
，∴0＜2α-
＜
，
∴cos(α-
)=
=
=
，（11分）
由cos(2α-
)=
得sin2α+cos2α=
②
①+②得2sin2α=
，
∴f(
+α)=
（14分）
解法3：由sin(2α-
)=
得sin2α-cos2α=
，（9分）
两边平方得1-sin4α=
，sin4α=
，
∵
＜α＜
∴
＜4α＜
，
∴cos4α=-
=-
，（11分）
∴sin22α=
=
，
又
＜2α＜
，∴sin2α=
，
∴f(
+α)=
．（14分）
| T |
| 2 |
| 7π |
| 8 |
| 3π |
| 8 |
| π |
| 2 |
又ω＞0，故ω=2，∴f（x）=2sin（2x+φ），（2分）
由f(
| 3π |
| 8 |
| 3π |
| 4 |
| π |
| 4 |
又-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 3π |
| 8 |
∴函数f（x）的单调增区间为[kπ-
| π |
| 8 |
| 3π |
| 8 |
（2）解法1：依题意得：2sin(2α-
| π |
| 4 |
| 6 |
| 5 |
| π |
| 4 |
| 3 |
| 5 |
∵
| π |
| 8 |
| 3π |
| 8 |
| π |
| 4 |
| π |
| 2 |
∴cos(2α-
| π |
| 4 |
1-sin2(2α-
|
1-(
|
| 4 |
| 5 |
f(
| π |
| 8 |
| π |
| 4 |
| π |
| 4 |
∵sin[(2α-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
7
| ||
| 10 |
f(
| π |
| 4 |
7
| ||
| 5 |
解法2：依题意得：sin(2α-
| π |
| 4 |
| 3 |
| 5 |
3
| ||
| 5 |
∵
| π |
| 8 |
| 3π |
| 8 |
| π |
| 4 |
| π |
| 2 |
∴cos(α-
| π |
| 4 |
1-sin2(2α-
|
1-(
|
| 4 |
| 5 |
由cos(2α-
| π |
| 4 |
| 4 |
| 5 |
4
| ||
| 5 |
①+②得2sin2α=
7
| ||
| 5 |
∴f(
| π |
| 8 |
7
| ||
| 5 |
解法3：由sin(2α-
| π |
| 4 |
| 3 |
| 5 |
3
| ||
| 5 |
两边平方得1-sin4α=
| 18 |
| 25 |
| 7 |
| 25 |
∵
| π |
| 8 |
| 3π |
| 8 |
| π |
| 2 |
| 3π |
| 2 |
∴cos4α=-
| 1-sin24α |
| 24 |
| 25 |
∴sin22α=
| 1-cos4α |
| 2 |
| 49 |
| 50 |
又
| π |
| 4 |
| 3π |
| 4 |
7
| ||
| 10 |
∴f(
| π |
| 8 |
7
| ||
| 5 |
点评：本题是基础题，由三角函数的图象确定函数的解析式，利用函数的解析式，求已知函数的三角函数值，求相关角的三角函数值，考查公式的灵活运用能力，化简能力，常考题目．
练习册系列答案
相关题目