题目内容
在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC,
(Ⅰ)求A的大小;
(Ⅱ)求sinB+sinC=1,试判断△ABC的形状。
(Ⅰ)求A的大小;
(Ⅱ)求sinB+sinC=1,试判断△ABC的形状。
解:(Ⅰ)由已知,根据正弦定理,得2a2=(2b+c)b+(2c+b)c,
即a2=b2+c2+bc,
由余弦定理,得a2=b2+c2-2bccosA,
故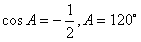 。
。
(Ⅱ)由(Ⅰ) ,得sin2A=sin2B+sin2C+sinBsinC,
又sinB+sinC=1,得sinB=sinC=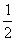 ,
,
因为0°<B<90°,0°<C<90°,
故B=C,
所以△ABC是等腰的钝角三角形。
即a2=b2+c2+bc,
由余弦定理,得a2=b2+c2-2bccosA,
故
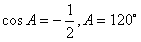 。
。 (Ⅱ)由(Ⅰ) ,得sin2A=sin2B+sin2C+sinBsinC,
又sinB+sinC=1,得sinB=sinC=
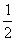 ,
,因为0°<B<90°,0°<C<90°,
故B=C,
所以△ABC是等腰的钝角三角形。

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|