题目内容

已知α、β∈(0,),a=(sinα,1-cosα),b=(sinβ,cosβ),且a·b=-cosα.

(1)求向量a与b的夹角θ;

(2)求α、β的值.

解：(1)｜a｜==2sin,｜b｜=1,                           

a·b=-cosα=-(1-2sin2)=+2sin2,

cosθ=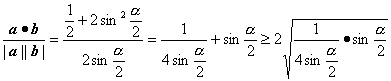=1,            

又0≤cosθ≤1,∴cosθ=1.

∵0≤θ≤π,∴θ=0.                                                           

(2)由(1),可知cosθ=1时,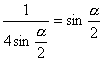,α∈(0,)                                

∴sin.∴.∴α=.                                               

将α=代入a·b=-cosα,得β=.

综上，α=β=.

练习册系列答案
相关题目
（2013•静安区一模）已知a＜0，关于x的不等式ax2-2（a+1）x+4＞0的解集是
(
2
a
，2)
(
2
a
，2)
．
（2013•金华模拟）已知a＞0，b＞0，a、b的等比中项是1，且m=b+
1
a
，n=a+
1
b
，则m+n的最小值是（　　）
（2013•揭阳二模）已知a＞0，函数f（x）=ax2-lnx．
（1）求f（x）的单调区间；
（2）当a=
1
8
时，证明：方程f(x)=f(
2
3
)在区间（2，+∞）上有唯一解；
（3）若存在均属于区间[1，3]的α，β且β-α≥1，使f（α）=f（β），证明：
ln3-ln2
5
≤a≤
ln2
3
．
已知a＞0，
1
b
-
1
a
＞1，求证：
1+a
＞
1
1-b
．
已知集合M={0，1}，N={y|y=x2+1，x∈M}，则M∩N=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网