题目内容
已知函数f(x)=log5(2x2+x),则f(x)的单调递减区间为
- A.(
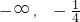 )
) - B.(
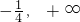 )
) - C.(
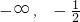 )
) - D.(0,+∞)
C
分析:根据f(x)=log5(2x2+x)可知,f(x)为复合函数,又复合函数的性质即可获得答案.
解答:∵f(x)=log5(2x2+x),
∴2x2+x>0,
∴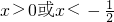 ,
,
令μ(x)=2x2+x,则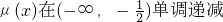 ,而y=log5x为定义域上的单调递增函数,
,而y=log5x为定义域上的单调递增函数,
由复合函数的单调性可知f(x)的单调递减区间为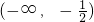 ,
,
故选C.
点评:本题考查对数函数的单调区间,关键是利用复合函数的性质解决,是容易题.
分析:根据f(x)=log5(2x2+x)可知,f(x)为复合函数,又复合函数的性质即可获得答案.
解答:∵f(x)=log5(2x2+x),
∴2x2+x>0,
∴
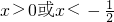 ,
,令μ(x)=2x2+x,则
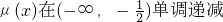 ,而y=log5x为定义域上的单调递增函数,
,而y=log5x为定义域上的单调递增函数,由复合函数的单调性可知f(x)的单调递减区间为
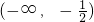 ,
,故选C.
点评:本题考查对数函数的单调区间,关键是利用复合函数的性质解决,是容易题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目