题目内容
3.求函数y=cos4x+2sin2xcos2x-cos2x+1的值域.分析 根据函数y的解析式,利用三角函数进行化简,求出它的值域即可.
解答 解:y=cos4x+2sin2xcos2x-cos2x+1
=(1-sin2x)cos2x+2sin2xcos2x-cos2x+1
=sin2xcos2x+1
=$\frac{1}{4}$(2sinxcosx)2+1
=$\frac{1}{4}$sin22x+1
=$\frac{1}{4}$×$\frac{1-cos4x}{2}$+1
=-$\frac{1}{8}$cos4x+$\frac{9}{8}$;
∵-1≤cos4x≤1,
∴-$\frac{1}{8}$≤-$\frac{1}{8}$cos4x≤$\frac{1}{8}$,
∴1≤-$\frac{1}{8}$cos4x+$\frac{9}{8}$≤$\frac{5}{4}$;
即函数y的值域是[1,$\frac{5}{4}$].
点评 本题考查了三角函数的图象与性质的应用问题,也考查了三角函数的恒等变换问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.设f(x)=lnx,0<a<b,若$p=f(\sqrt{ab})$,$q=f(\frac{a+b}{2})$,r=$\frac{f(a)+f(b)}{2}$,则下列关系式中正确的是( )
| A. | p=r<q | B. | q=r>p | C. | p=r>q | D. | q=r<p |
18.设A={x|y=$\sqrt{2-x}$},B={x|y=ln(x2-1)},则A∩∁UB=( )
| A. | {x|x>-2} | B. | {x|1<x≤2} | C. | {x|-1≤x≤1} | D. | ∅ |
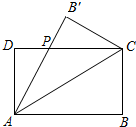 春兰公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能.
春兰公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能.