Question

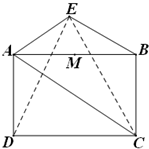（2013•东城区模拟）如图，四边形ABCD为矩形，AD⊥平面ABE，AE=BE=2，AB=2

2

．
（Ⅰ）求证：AE⊥CE；
（Ⅱ）设M是线段AB的中点，试在线段CE上确定一点N，使得MN∥平面ADE．

Answer 1

分析：（I）根据勾股定理的逆定理，证出AE⊥BE．由AD⊥平面ABE得到AD⊥AE，结合AD∥BC证出BC⊥AE，从而得出AE⊥平面BCE，结合CE?平面BCE可得AE⊥CE．
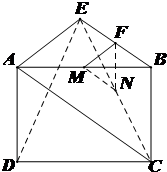
（II）设BE的中点为F，CE的中点为N，连接MN、MF、NF．利用三角形的中位线定理，证出MF∥AE且NF∥AD，再用线面平行判定定理，证出MF∥平面ADE且NF∥平面ADE，再根据面面平行判定定理证出平面MNF∥平面ADE，进而得到MN∥平面ADE．由此可得当N为CE中点时，MN∥平面ADE．

解答：解：（Ⅰ）∵AE=BE=2，AB=2

2

，
∴AE²+BE²=8=AB²，可得AE⊥BE．----------------------（2分）
∵AD⊥平面ABE，AE?平面ABE，
∴AD⊥AE，结合AD∥BC可得BC⊥AE，---------------------（4分）
又∵BC、BE是平面BCE内的相交直线，
∴AE⊥平面BCE，结合CE?平面BCE，可得AE⊥CE．----------------------（6分）
（Ⅱ）设BE的中点为F，CE的中点为N，连接MN、MF、NF，----（7分）
∵△ABE中，M、F分别是AB、BE的中点，
∴MF∥AE，同理可得NF∥BC∥AD．
∵MF?平面ADE，AE?平面ADE，
∴MF∥平面ADE．-----------------------------（9分）
同理可证NF∥平面ADE，
又∵MF、NF是平面MNF内的相交直线，∴平面MNF∥平面ADE，
∵MN?平面MNF，∴MN∥平面ADE．----------------------------（12分）
由此可得：当N为CE中点时，MN∥平面ADE．------（13分）

点评：本题在四棱锥E-ABCD内证明线线垂直，并探索线面平行的问题．着重考查了直线与平面垂直的判定与性质，线面平行、面面平行的判定与性质等知识，属于中档题．