题目内容
过点M(-2,0)的直线l与椭圆x2+2y2=2交于P1、P2两点,线段P1P2的中点为P,设直线l的斜率为k(k≠0),OP斜率为k′.(1)证明k×k′为定值;
(2)求△OMP面积的取值范围.
(1)证明:设P(x1,y1),P2(x2,y2),代入椭圆作差得![]() ×
×![]() =-
=-![]() ,
,
即k×k′=-![]() .
.
(2)解:S△OMP=![]() |OM|×|yP|=|yP|=|
|OM|×|yP|=|yP|=|![]() |,
|,
把y=k(x+2)代入椭圆x2+2y2=2,
消去x得![]() y2-
y2-![]() y+2=0, ①
y+2=0, ①
由根与系数的关系得![]() =
=![]() ,
,
∴S△OMP=![]() =
=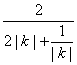 ≤
≤![]() ,
,
等号在2|k|=![]() ,即k=±
,即k=±![]() 时成立,此时方程①的Δ=0,即直线与椭圆相切,不合题意,
时成立,此时方程①的Δ=0,即直线与椭圆相切,不合题意,
∴△OMP面积的取值范围是(0,![]() ).
).

练习册系列答案
相关题目

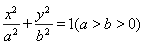
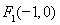



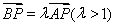
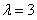
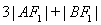
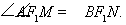
 (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆 上.
上.