题目内容
设直线l:y=3x-2与椭圆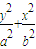 =1(a>b>0)相交于A、B两点,且弦AB的中点M在直线x+y=0上,则椭圆的离心率为( )
=1(a>b>0)相交于A、B两点,且弦AB的中点M在直线x+y=0上,则椭圆的离心率为( )A.
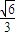
B.

C.
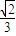
D.
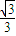
【答案】分析:根据题意,设出A、B点及其中点的坐标,与中点坐标公式和直线的斜率计算公式联系,由点差法,可得 =3;结合椭圆的离心率的计算方法e=
=3;结合椭圆的离心率的计算方法e= =
= ;代入a、b的关系可得答案.
;代入a、b的关系可得答案.
解答:解:A(x1,y1),B(x2,y2),有KAB= =3;
=3;
设AB的中点为M,其坐标为(m,n),则(x1+x2)=2m,(y1+y2)=2n;
又由弦AB的中点M在直线x+y=0上,即m+n=0,
A、B两点在椭圆上,
则 =1,①
=1,①
 =1,②;
=1,②;
①-②可得, (y1+y2)(y1-y2)=-
(y1+y2)(y1-y2)=- (x1+x2)(x1-x2);
(x1+x2)(x1-x2);
化简可得: =3;
=3;
则椭圆的离心率为e= =
= ;
;
故选A.
点评:本题考查直线与椭圆的综合运用,注意点差法的运用,即设而不求的方法;一般用于已知斜率与中点坐标两者之一或两者都已知或未知,进而求解求解其它参数(离心率)的情况.
 =3;结合椭圆的离心率的计算方法e=
=3;结合椭圆的离心率的计算方法e= =
= ;代入a、b的关系可得答案.
;代入a、b的关系可得答案.解答:解:A(x1,y1),B(x2,y2),有KAB=
 =3;
=3;设AB的中点为M,其坐标为(m,n),则(x1+x2)=2m,(y1+y2)=2n;
又由弦AB的中点M在直线x+y=0上,即m+n=0,
A、B两点在椭圆上,
则
 =1,①
=1,① =1,②;
=1,②;①-②可得,
 (y1+y2)(y1-y2)=-
(y1+y2)(y1-y2)=- (x1+x2)(x1-x2);
(x1+x2)(x1-x2);化简可得:
 =3;
=3;则椭圆的离心率为e=
 =
= ;
;故选A.
点评:本题考查直线与椭圆的综合运用,注意点差法的运用,即设而不求的方法;一般用于已知斜率与中点坐标两者之一或两者都已知或未知,进而求解求解其它参数(离心率)的情况.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
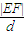 的最大值.并求出此时b的值.
的最大值.并求出此时b的值. 的最大值.并求出此时b的值.
的最大值.并求出此时b的值.