题目内容

抛物线y2=2px（p＞0）有一内接直角三角形，直角的顶点在原点，一直角边的方程是y=2x，斜边长是5，求此抛物线方程.?

思路分析：可由三角形的边的方程与抛物线方程构造方程组解出三角形的顶点坐标，结合斜边长求出p.?

解：设△AOB为抛物线的内接直角三角形，直角顶点为O，AO边的方程是y=2x，?

则OB边方程为y=-x.?

由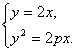可得A点坐标为（,p）,?

由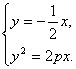可得B点坐标为（8p,-4p）.

∵|AB|=5,

∴=5.

∵p＞0,解得p=,?

∴所求的抛物线方程为y2=x.

温馨提示

求抛物线的标准方程.即求p的值和确定开口方向.因而如何根据已知条件建立起关于p的方程是解决本题的关键.

练习册系列答案
相关题目
精英家教网如图过抛物线y2=2px（p＞0）的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=3，则抛物线的方程为（　　）
A、y2=
3
2
x
B、y2=9x
C、y2=
9
2
x
D、y2=3x
抛物线y2=2px（p＞0）上的点M（4，y）到焦点F的距离为5，O为坐标原点，则△OFM的面积为
2
2
．
抛物线y2=2px，（p＞0）绕焦点依逆时针方向旋转90°所得抛物线方程为…（　　）
（2012•泉州模拟）若抛物线y2=2px（p＞0）的焦点到双曲线x2-y2=1的渐近线的距离为
3
2
2
，则p的值为（　　）
过点A（-1，0）作抛物线y2=2px（p＞0）的两条切线，切点分别为B、C，且△ABC是正三角形，则抛物线方程为
y2=
4
3
x
y2=
4
3
x
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网