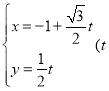题目内容
【题目】已知函数
的图象经过点
（1，1），
．
（1）求函数
的解析式；
（2）判断函数
在（0，+
）上的单调性并用定义证明；
（3）求在区间
上的值域；
【答案】（1）
（2）函数在（0，+
）上为减函数（3）
【解析】
试题分析：（1）将点的坐标代入函数式可得到关于
的关系式，解方程可求得其值，从而确定函数解析式；（2）判断函数单调性，首先假设
，在此基础上判断
的大小关系，从而确定单调性；（3）由函数的单调性可确定函数在
上的最大值和最小值，从而求得值域
试题解析：（1） 由 f(x)的图象过A、B，则
，解得
．
∴ ……4分
（2）证明：设任意x1，x2∈（0，+），且x1<x2．
∴
.
由x1，x2∈（0，+），得x1x2>0，x1x2+2>0．
由x1<x2，得
．
∴
，即
．
∴函数
在（0，+）上为减函数．
（3）
函数
在（0，+
）上为减函数
.
练习册系列答案
相关题目
