Question

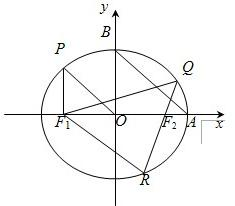如图，过椭圆

x2

a2

+

y2

b2

=1 (a＞b＞0)的左焦点F₁作x轴的垂线交椭圆于点P，
点A和点B分别为椭圆的右顶点和上顶点，OP∥AB．
（1）求椭圆的离心率e；
（2）过右焦点F₂作一条弦QR，使QR⊥AB．若△F₁QR的面积为20

3

，求椭圆的方程．

Answer 1

分析：（1）由于F₁（-c，0），P(-c，

b2

a

)．且OP∥AB，根据直线的斜率相等得到：k_OP=k_AB解得：b=c．从而a=

2

c，即可求得椭圆的离心率e；
（2）由（1）知椭圆方程可化简为x²+2y²=2b²．①易求直线QR的斜率为

2

，故可设直线QR的方程为：y=

2

(x-b) 将直线的方程代入椭圆的方程，消去y得到关于x的一元二次方程，再结合根系数的关系利用弦长公式即可求得b值，从而解决问题．

解答：解：（1）∵F₁（-c，0），∴P(-c，

b2

a

)．
∵OP∥AB，∴k_OP=k_AB，∴

b2 a

c

=

b

a

，
解得：b=c．∴a=

2

c，故e=

2

2

．
（2）由（1）知椭圆方程可化简为x²+2y²=2b²．
①易求直线QR的斜率为

2

，故可设直线QR的方程为：y=

2

(x-b)．②
由①②消去y得：5x²-8bx+2b²=0．
∴x1+x2=

8b

5

，x1x2=

2b2

5

．
于是△F₁QR的面积S=c•|y1-y2|=

2

c•|x1-x2|=

2

b•

(x1+x2)2-4x1x2

=

2

b•

( 8b 5 )2-4× 2b2 5

=

4 3

5

b2=20

3

，∴b=5．因此椭圆的方程为x²+2y²=50，即

x2

50

+

y2

25

=1

点评：本题主要考查了椭圆的简单性质，椭圆的标准方程，解题的关键是要求考生对椭圆基础知识的熟练掌握．