题目内容
已知点M是圆C: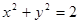 上的一点,且
上的一点,且
 轴,
轴, 为垂足,点
为垂足,点 满足
满足 ,记动点
,记动点 的轨迹为曲线E.
的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)若AB是曲线E的长为2的动弦,O为坐标原点,求 面积S的最大值.
面积S的最大值.
(Ⅰ) (Ⅱ)
(Ⅱ)
解析试题分析:(Ⅰ)设N(x,y),M( ),则由已知得,
),则由已知得, ,
, , 2分
, 2分
代入 得,
得, . 4分
. 4分
所以曲线E的方程为 . 5分
. 5分
(Ⅱ)方法一:
因为线段 的长等于椭圆短轴的长,要使三点
的长等于椭圆短轴的长,要使三点 能构成三角形,
能构成三角形,
则弦 不能与
不能与 轴垂直,故可设直线
轴垂直,故可设直线 的方程为
的方程为 ,
,
由 ,消去
,消去 ,并整理,得
,并整理,得 . 7分
. 7分
设 ,
, ,又
,又 ,
,
所以 ,
, , 9分
, 9分
因为 ,
,
所以 ,即
,即 ,
,
所以 ,即
,即 ,
,
因为 ,所以
,所以 . 12分
. 12分
又点 到直线
到直线 的距离
的距离 ,
,
因为
 ,
,
所以

 14分
14分
所以 ,即
,即 的最大值为
的最大值为 . 15分
. 15分
(Ⅱ)方法二:
因为线段 的长等于椭圆短轴的长,要使三点
的长等于椭圆短轴的长,要使三点 能构成三角形,
能构成三角形,
则弦 不能与
不能与 垂直,故可设直线
垂直,故可设直线 的方程为
的方程为 ,
,
由
练习册系列答案
相关题目
 (α为参数).
(α为参数).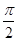 ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;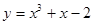 在点
在点 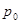 处的切线
处的切线 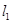 平行直线
平行直线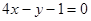 ,且点
,且点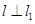 , 且
, 且 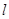 也过切点
也过切点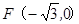 ,且过点
,且过点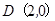 .
.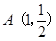 ,若
,若 是椭圆上的动点,求线段
是椭圆上的动点,求线段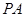 的中点
的中点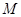 的轨迹方程.
的轨迹方程.  轴上,长轴长等于12,离心率等于
轴上,长轴长等于12,离心率等于 ;椭圆经过点
;椭圆经过点 ;椭圆的一个焦点到长轴两端点的距离分别为10和4.
;椭圆的一个焦点到长轴两端点的距离分别为10和4.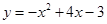 与它在点
与它在点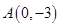 和点
和点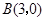 的切线所围成的区域的面积。
的切线所围成的区域的面积。 的离心率为
的离心率为 ,且过点
,且过点 .
.
 ,
, 的最值.
的最值. ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 ,求直线
,求直线 的方程.
的方程. (
( .
.
 ,求椭圆的标准方程;
,求椭圆的标准方程; 的直线
的直线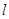 与椭圆C交于不同的两点
与椭圆C交于不同的两点 ,且
,且 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线 )相交于
)相交于 四点,设原点
四点,设原点 一边的距离为
一边的距离为 ,试求
,试求 时
时 满足的条件.
满足的条件.