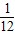Question

将三粒均匀的分别标有：1，2，3，4，5，6的正六面体骰子同时掷出，出现的数字分别为a，b，c，则a，b，c正好是直角三角形三边长的概率是（　　）

• A、

  1

  6

• B、

  1

  12

• C、

  1

  36

• D、

  5

  36

Answer 1

分析：本题是一个由三步才能完成的事件，共有6×6×6=216种结果，a，b，c正好是直角三角形三边长，则它们应该是一组勾股数，在这216组数中，找出勾股数的情况，因而得出是直角三角形三边长的概率即可．

解答：解：共有6×6×6=216种结果，每种结果出现的机会相同，a，b，c正好是直角三角形三边长，则它们应该是一组勾股数，在这216组数中，是勾股数的有3，4，5；3，5，4；4，3，5；4，5，3；5，3，4；5，4，3共6中情况，因而a，b，c正好是直角三角形三边长的概率是

6

216

=

1

36

．
P（a，b，c正好是直角三角形三边长）=

6

216

=

1

36

．
故选C．

点评：本题主要考查了等可能事件的概率，属于基础题，用到的知识点为：概率等于所求情况数与总情况数之比；3，5.4为三角形三边的三角形是直角三角形．