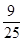题目内容
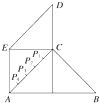
两个等腰直角三角形ABD、CBD中, ∠ADB=∠CBD=90°, 且它们所在平面互相垂 直, 在AB上取一点P, 使△PCD所在平面与△BCD所在平面所成的二面角为60°. 指出此时P分BA的比的平方值, 即PB2:PA2=_______.
答案:3:2
解析:
提示:
解析:
|
解: 过P作PE⊥BD于E, ∵ 平面ABD⊥平面CBD, ∴ PE⊥平面BCD, 过E作EF⊥CD, 连PF, 则PF⊥CD, ∴ ∠PFE为二面角P-CD-B的平面角. 设∠PFE=60° EF=a 在等腰△DBE中∠BDC=45°
又 ∵ ∠EFD=90°, ∴ DF=a, DE=
在Rt△PEF中, ∠PFE=60°, ∴ PF=2a, PE=
∴ BE= 在等腰Rt△ADB中,
AB=(
∴ 当P点分BA的比为 △PCD与△BCD所在平面所成的二面角为60°. |
提示:
| 作PE⊥BD于E, 过E作EF⊥CD于F, 连PF, 证明∠PFE为二面角P-CD-B的平面角. |

练习册系列答案
相关题目
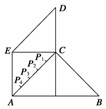
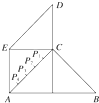 某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,则转播台应建在( )
某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,则转播台应建在( )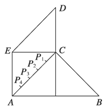
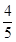 B.
B.
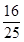
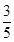 D.
D.