题目内容
若α、β为锐角,且cosα= ,sinβ=
,sinβ= ,则α+β= .
,则α+β= .

解析试题分析:∵ ,α是锐角,
,α是锐角, ,又
,又 ,β是锐角,
,β是锐角, ,
,
∴cos(α+β)=cosαcosβ-sinαsinβ= ,∵0<α<90°,0<β<90°,∴0<α+β<180°,∴α+β=135°故应填入: 135°.
,∵0<α<90°,0<β<90°,∴0<α+β<180°,∴α+β=135°故应填入: 135°.
考点:1.同角三角函数的基本关系式;2.两角和与差的三角函数.

练习册系列答案
相关题目
已知sin 2α=- ,α∈
,α∈ ,则sin α+cos α=
,则sin α+cos α=
A.- | B. | C.- | D. |
已知函数f(x)=Acos(ωx+ )(x∈R)的图像的一部分如下图所示,其中A>0,ω>0,|
)(x∈R)的图像的一部分如下图所示,其中A>0,ω>0,| |<
|< ,为了得到函数f(x)的图像,只要将函数g(x)=
,为了得到函数f(x)的图像,只要将函数g(x)= (x∈R)的图像上所有的点( )
(x∈R)的图像上所有的点( ) 
A.向右平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
B.向右平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移 个单位长度,再把得所各点的横坐标缩短到原来的 个单位长度,再把得所各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
若 ,则
,则 的值为( )
的值为( )
A. | B.- | C. | D. |
 =2,则
=2,则 的值为
的值为 ;
; 的值为
的值为
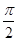 的扇形的内接矩形OABC(只有B在弧上)的面积的最大值= .
的扇形的内接矩形OABC(只有B在弧上)的面积的最大值= .
 ;
; ,
, 的值域是 .
的值域是 . =_________.
=_________.