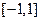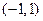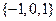题目内容
设集合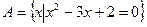 ,
,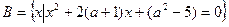
(1)若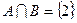 ,求实数
,求实数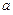 的值;
的值;
(2)若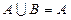 ,求实数
,求实数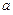 的取值范围
的取值范围
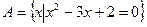 ,
,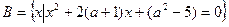
(1)若
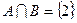 ,求实数
,求实数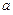 的值;
的值;(2)若
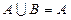 ,求实数
,求实数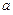 的取值范围
的取值范围(1)  或
或 (2) 实数
(2) 实数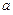 的取值范围是
的取值范围是
 或
或 (2) 实数
(2) 实数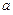 的取值范围是
的取值范围是
对于含参数的集合的运算,首先解出不含参数的集合,然后根据已知条件求参数。
因为 ,
,
(1)由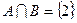 知,
知, ,从而得
,从而得 ,即
,即
 ,解得
,解得 或
或
当 时,
时, ,满足条件;
,满足条件;
当 时,
时, ,满足条件
,满足条件
所以 或
或
(2)对于集合 ,由
,由
因为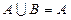 ,所以
,所以
①当 ,即
,即 时,
时, ,满足条件;
,满足条件;
②当 ,即
,即 时,
时, ,满足条件;
,满足条件;
③当 ,即
,即 时,
时, 才能满足条件,
才能满足条件,
由根与系数的关系得 ,矛盾
,矛盾
故实数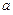 的取值范围是
的取值范围是
对于比较抽象的集合,在探究它们的关系时,要先对它们进行化简。同时,要注意集合的子集要考虑空与不空,不要忘了集合本身和空集这两种特殊情况.
因为
 ,
,(1)由
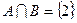 知,
知, ,从而得
,从而得 ,即
,即 ,解得
,解得 或
或
当
 时,
时, ,满足条件;
,满足条件;当
 时,
时, ,满足条件
,满足条件所以
 或
或
(2)对于集合
 ,由
,由
因为
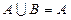 ,所以
,所以
①当
 ,即
,即 时,
时, ,满足条件;
,满足条件;②当
 ,即
,即 时,
时, ,满足条件;
,满足条件;③当
 ,即
,即 时,
时, 才能满足条件,
才能满足条件,由根与系数的关系得
 ,矛盾
,矛盾故实数
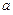 的取值范围是
的取值范围是
对于比较抽象的集合,在探究它们的关系时,要先对它们进行化简。同时,要注意集合的子集要考虑空与不空,不要忘了集合本身和空集这两种特殊情况.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 ,
, .若
.若 ,求实数
,求实数 的取值范围.
的取值范围.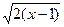 },B={x|x2–ax≤x–a},当A
},B={x|x2–ax≤x–a},当A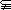 B时,则a的取值范围是 .
B时,则a的取值范围是 . ,
, ,那么集合
,那么集合 为( )
为( ) ;
; ;
; ;
;
 ,集合
,集合
 ;
; ,求
,求 的取值范围。
的取值范围。 ,
, ,
, ,记
,记 ,
, ,则
,则 =( )
=( ) ;
; ;
; ;
;
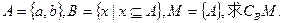
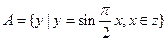 ,集合
,集合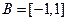 ,则
,则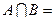 ( )
( )