题目内容
(本小题10分)
设 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)点 为当
为当 时轨迹E上的任意一点,定点
时轨迹E上的任意一点,定点 的坐标为(3,0),
的坐标为(3,0),
点 满足
满足 ,试求点
,试求点 的轨迹方程。
的轨迹方程。
【答案】
(1) 当m=0时,方程表示两直线,方程为 ;
;
当 时, 方程表示的是圆
时, 方程表示的是圆
当 且
且 时,方程表示的是椭圆
时,方程表示的是椭圆
(2) 
【解析】解:(1)因为 ,
, ,
, ,
,
所以 , 即
, 即 . w.w.w.k.s.5.u.c.o.m
. w.w.w.k.s.5.u.c.o.m 

当m=0时,方程表示两直线,方程为 ;
;
当 时, 方程表示的是圆
时, 方程表示的是圆
当 且
且 时,方程表示的是椭圆;
时,方程表示的是椭圆;
当 时,方程表示的是双曲线.
时,方程表示的是双曲线.
(2)设
, ,
,
当 时,轨迹E为
时,轨迹E为 ,点
,点
所以点 的轨迹方程为
的轨迹方程为 。
。

练习册系列答案
相关题目
 ,
, ,
, .
. ,求
,求 的值;
的值;  ,求函数
,求函数 的值域.
的值域. ,
,
 .
. 的各项均为正值,首项
的各项均为正值,首项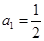 ,前n项和为
,前n项和为 ,且
,且
 的前n项和
的前n项和
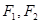 分别为椭圆
分别为椭圆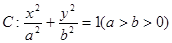 的左、右两个焦点.(1)若椭圆
的左、右两个焦点.(1)若椭圆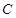 上的点
上的点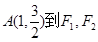 两点的距离之和等于4,求椭圆
两点的距离之和等于4,求椭圆 。
。 :对任意实数x,不等式
:对任意实数x,不等式 恒成立;命题
恒成立;命题 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线.(1)若命题
轴上的双曲线.(1)若命题 的取值范围;(2)若命题:
的取值范围;(2)若命题:  为真命题,且“
为真命题,且“ ”为假命题,求实数m的取值范围.
”为假命题,求实数m的取值范围.