Question

已知函数f（x）=C_n⁰x^2n-1-C_n¹x²ⁿ+C_n¹x²ⁿ⁺¹-…+C_n^r（-1）^rx^2n-1+r+…+C_nⁿx^3n-1，其中n（n∈N₊）．
（1）求函数f（x）的极大值和极小值；
（2）设函数f（x）取得极大值时x=a_n，令b_n=2-3a_n，S_n=b₁b₂+b₂b₃+…+b_nb_n+1，若p≤S_n＜q对一切n∈N₊恒成立，求实数p和q的取值范围．

Answer 1

分析：（1）利用二项式定理化简f（x），求出导函数，令导函数为0求根，判断根两侧的导函数符号，求出极值．
（2）利用数列的求和方法：裂项法求出S_n，求出S_n的范围即为p，q值．

解答：解：（1）f（x）=x^2n-1[C_n⁰-C_n¹x+C_n²x²-+C_n^r（-1）^rx^r+C_nⁿxⁿ]=x^2n-1（1-x）ⁿ，
f'（x）=（2n-1）x^2n-2（1-x）ⁿ-x^2n-1•n（1-x）^n-1=x^2n-2（1-x）^n-1[2n-1-（3n-1）x]．
令f'（x）=0x1=0，x2=

2n-1

3n-1

，x3=1，从而x₁＜x₂＜x₃．当n为偶数时f（x）的增减如下表

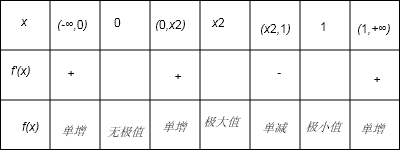
所以当x=

2n-1

3n-1

时，y_极大=

(2n-1)2n-1•nn

(3n-1)3n-1

；当x=1时，y_极小=0．
当n为奇数时f（x）的增减如下表

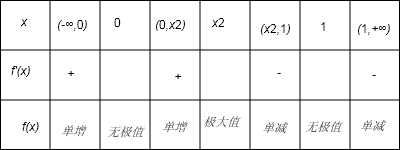
所以当x=

2n-1

3n-1

时，y_极大=

(2n-1)2n-1•nn

(3n-1)3n-1

．
（2）由（1）知f（x）在x=

2n-1

3n-1

时取得最大值．所以a_n=

2n-1

3n-1

，b_n=2-3a_n=

1

3n-1

，bnbn+1=

1

(3n-1)(3n+2)

=

1

3

(

1

3n-1

-

1

3n+2

)Sn=

1

3

[(

1

2

-

1

5

)+(

1

5

-

1

8

)++(

1

3n-1

-

1

3n+2

)]=

1

6

-

1

3(3n+2)

＜

1

6

．n∈N+∴0＜

1

3(3n+2)

≤

1

15

，∴-

1

15

≤

1

3(3n+2)

＜0，即

1

10

≤

1

6

-

1

3(3n+2)

＜

1

6

；
所以实数p和q的取值范围分别是p∈(-∞，

1

10

]，q∈[

1

6

．+∞)．

点评：本题考查，二项式定理；利用导数求函数的单调性，极值；利用裂项法求数列的和；求函数的值域等