题目内容
已知f(x)是定义在(-∞,+∞)上的不恒为零的函数,且对定义域内的任意x、y,f(x)都满足f(xy)=yf(x)+xf(y).
(1)求f(1)、f(-1)的值;
(2)判断f(x)的奇偶性,并说明理由.
答案:
解析:
提示:
解析:
|
解:(1)∵f(x)对任意x、y都有f(x·y)=yf(x)+xf(y), ∴令x=y=1时,有f(1·1)=1·f(1)+1·f(1). ∴f(1)=0. ∴令x=y=-1时,有f[(-1)·(-1)]=(-1)·f(-1)+(-1)·f(-1). ∴f(-1)=0. (2)∵f(x)对任意x,y都有f(x·y)=yf(x)+xf(y), ∴令y=-1,有f(-x)=-f(x)+xf(-1). 将f(-1)=0代入,得f(-x)=-f(x), ∴函数f(x)是(-∞,+∞)上的奇函数. |
提示:
|
(1)利用赋值法,令x=y=1得f(1)的值,令x=y=-1,得f(-1)的值;(2)利用定义法证明f(x)是奇函数,要借助于赋值法得f(-x)=-f(x). |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 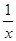 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
